Постройте график функции y=f(x) по результатам исследования.
1.
2. Функция нечëтная
3. а) График функции пересекает ось ОХ в точках (-6;0) (0;0) (6;0)
б) График функции пересекает ось ОY в точке (0;0)
4.
5,6(на фото)
7.
8.
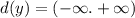
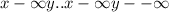
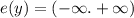

Другие вопросы по теме Алгебра
Популярные вопросы
- Какие имена у трех богатырей былинных...
2 - Выпишите только те слова,которые состоят из твёрдых звуков.докажите...
2 - 25 за ответ 2 3/5 × 1 9/26= 7/19 × 57 = 25 за ответ...
2 - Выписать все словосочетания 1)он зашумел тростником, бросил в воду...
3 - Форма сустава- локтевого и коленного и возможные движения (биология...
1 - Что лишнее и почему? , пуритане, кальвинисты, лютеране, иезуиты....
2 - Существует метод шифрования - шифрованмя с ключа. таким образом,...
2 - Найдите наименьшое общее кратное чисел , разложив их на простые множители...
1 - Между какими материками расположен тихий океан и с какими связан...
2 - Какие растение и животные занесены в красную книгу нашего края...
1
1. Дано: d(y) = (-∞, +∞)
Обоснование: Из данного уравнения видно, что функция не определена нижней или верхней границами, то есть неограничена снизу и сверху. Это означает, что график функции будет растягиваться на всей оси y.
Решение: Нет необходимости в пошаговом решении, так как это указывает на характер функции.
2. Дано: Функция нечетная
Обоснование: Если функция является нечетной, это означает, что f(-x) = -f(x). Это означает, что точки графика функции будут симметричны относительно начала координат.
Решение: Нет необходимости в пошаговом решении, так как это указывает на характер функции.
3.а) Дано: График функции пересекает ось ОХ в точках (-6;0), (0;0), (6;0)
Обоснование: Из данного условия видно, что функция пересекает ось ОХ в трех точках, что означает у функции есть три корня или нулевые значения.
Решение:
- Начнем с построения оси ОХ и отметим точки (-6;0), (0;0), (6;0) на оси ОХ.
- Нарисуем горизонтальную прямую через эти три точки. Это будет горизонтальная линия на уровне y = 0.
- Это будет график функции, который пересекает ось ОХ в указанных точках.
3.б) Дано: График функции пересекает ось ОY в точке (0;0)
Обоснование: По условию видно, что функция пересекает ось ОY в точке (0;0), что означает у функции есть один корень или нулевое значение.
Решение:
- Начнем с построения оси ОХ и оси ОY.
- Отметим точку (0;0) на оси ОY.
- Это будет график функции, который пересекает ось ОY в указанной точке.
4. Дано: Не указано
Обоснование: Не указано никакой информации о характере функции.
Решение: График функции в данном случае будет неопределен.
5,6. Дано: На фото
Обоснование: Нет информации о характере функции или точках пересечения с осями.
Решение: Не получается построить график функции без дополнительной информации.
7. Дано: x → -∞, y → -∞
Обоснование: Из данного уравнения видно, что по мере того, как значение x стремится к отрицательной бесконечности, значение y также стремится к отрицательной бесконечности.
Решение: Нет необходимости в пошаговом решении, так как это указывает на характер функции.
8. Дано: e(y) = (-∞, +∞)
Обоснование: Из данного уравнения видно, что функция e(y) неограничена сверху и снизу. Это означает, что график функции будет растягиваться на всей оси y.
Решение: Нет необходимости в пошаговом решении, так как это указывает на характер функции.
Объединяя все информацию, полученную из данного исследования, график функции y=f(x) будет иметь следующие характеристики:
- Функция неограничена сверху и снизу (d(y) = (-∞, +∞)).
- Функция будет нечетной.
- График функции пересечет ось ОХ в точках (-6;0), (0;0), (6;0).
- График функции пересечет ось ОY в точке (0;0).
Остальные пункты не содержат достаточной информации для построения графика функции.