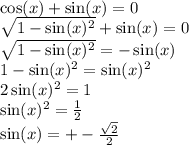 Почему только один из корней подходит в уравнение, если оба корня входят в одз?
Почему только один из корней подходит в уравнение, если оба корня входят в одз?
Другие вопросы по теме Алгебра
Популярные вопросы
- Решите показательное уравнение 2^(3x+10)-3^(3x+9)+3^(3x+7)+2^(3x+9)=0...
2 - Вчём сходство творчества писателя и...
1 - Треба написати про байрона по епіграфу мій дух як ніч...
1 - Роман не стал рассказывать страх, как требовательны были к нему его собственные...
2 - Решите неравенство 2lg(x+2) lg(x+4) нужно решение, одз, проверка, координатная прямая....
2 - Выписать 5 предложений с деепричастными оборотами из произведения л.н.толстого детство...
1 - Назовите схему решения системы линейных уравнений по методу гаусса....
2 - Перечисли необходимые условия жизни растений...
1 - Електричний чайник розрахований на 127 в і силу струму 5,3 а. який додатковий опір...
3 - He hasn,t . pupils have got вставь much many a lot of...
3
Это однородное уравение первой степени Решается оно делением обеих частей на Cosx , Cosx ≠ 0 .