Очень . Даю 100 б. Постройте график функции (см. ниже) И определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
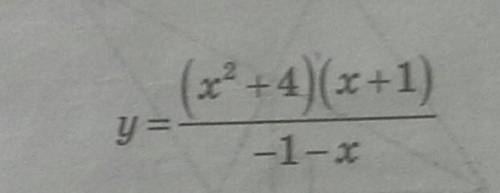
Другие вопросы по теме Алгебра
Популярные вопросы
- за такое задание мне вам на заранее...
3 - Выполните самостоятельную работу1. Из предложенных уравнений...
1 - В.В. МАЯКОВСКИЙ «ЛЮБЛЮ» (ОТРЫВОК ИЗ ПОЭМЫ) 1 Прочитайте выразительно...
1 - Укажіть усі значення x, при яких не має змісту рівняння:11 6...
1 - Вероятность появления события в каждом из независимых испытаний...
1 - сзади меня сидят два бандита и если я не решу это задание меня...
2 - Чем были набиты койка и матрац Джек Лондон ,,Любовь к жизни``...
2 - What he (to read) tomorrow...
2 - Производятся последовательные независимые испытания приборов...
1 - А координатной плоскости отложены точки с разными значениями...
2
В решении.
Объяснение:
1) Постройте график функции у = ((x²+4)*(x+1))/(-1-x).
Преобразовать уравнение для упрощения:
((x² + 4)*(x + 1))/(-1 - x) = ((x² + 4)*(x + 1))/ -(1 + x) =
Сократить числитель и знаменатель на (х + 1);
= (х² + 4)/ (-1) = -х² - 4;
у = -х² - 4;
Уравнение квадратичной функции, график - парабола со смещённым центром, ветви направлены вниз.
ОДЗ: х ≠ -1 (при этом значении х знаменатель дроби равен нулю, функция не определена).
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
Таблица:
х -2 -1 0 1 2
у -8 -5 -4 -5 -8
Следует иметь ввиду, что график хоть и строится по вычисленным точкам, точка с координатами (-1; -5) является "выколотой", функция в этой точке не существует.
2) Определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Прямая y = kx имеет с графиком ровно одну общую точку, если проходит через указанную "выколотую" точку.
Найти уравнение этой прямой.
Вычислить значение k. Для этого в уравнение подставить известные значения х и у (координаты "выколотой" точки):
y = kx
-5 = k * (-1)
-5 = -k
k = 5;
Уравнение прямой:
у = 5х;
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу. График - прямая линия, проходящая через начало координат.
Таблица:
х -1 0 1
у -5 0 5
При k = 5 прямая y = kx имеет с графиком ровно одну общую точку.