Объясните подробно, как делать подобные : найдите значение выражения: квадратный корень 8-2√7(здесь корень заканчивается)-√7

тут мы иммем дело с разницей квадрата под корнем. его надо уметь видеть.

=  + 2ab + 

=  - 2ab + 

в данном случе второе(минус перед два корней из семи).

И так 2√7 - в данном случае это у нас 2ab.

8 - это сума а в квадрате и б в квадрате.

то есть:

8 =   +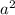 

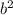
2ab = 2√7

ab = √7

То есть нам нужно методом подбора подобрать такие числа, чтобы их сумма в квадрате была 8, а при умножении они давали корень из семи. (тут метод подбора ничего более просто нужны тренировки и практика для этого).

Я подобрала:

и 1. И в правду, * 1 =[/tex]\sqrt{7}[/tex]

и  + 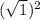 = 7 + 1 = 8

то есть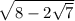  = 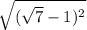 = | 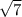- 1| (по модулю, модуль убираем, ибо |

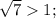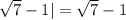
То есть:

=   - 1  - = -1.

ответ: -1.