Нужно решить по теореме виета
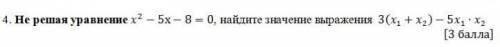
Другие вопросы по теме Алгебра
Популярные вопросы
- На диаграмме показано содержание питательных веществ в сухарях. определите...
3 - Вычислите сумму последовательных натуральных чисел от 1 до 99...
3 - Написать сочинение по своему фото...
1 - Предложения бывают по цели высказывания и повествовательное вопросительное...
1 - Подписи по этими картинками перепутаны. подбери и напиши правильную подпись...
3 - Под всеми буквами. информатика 8 класс...
1 - Наменателю (4 дроби к наименьшему общему знаме461).159. 1с | сои3) вин;...
1 - Дайте определение классификации. нарисуйте 2 примера форм классификации....
1 - Пример 42 плюс скобка открывается минус 26 скобка закрывается минус минус...
3 - Пересечение поверхностей, одна проецирующая....
3
55
Объяснение:
Согласно теореме Виета, сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а их произведение равно свободному члену, то есть:
х₁ + х₂ = - (-5) = 5
х₁ · х₂ = - 8.
Следовательно:
3(х₁ + х₂) = 3 · 5 = 15
5х₁ · х₂ = 5 · (-8) = - 40
3(х₁ + х₂) - 5х₁ · х₂ = 15 - (-40) = 15 + 40 = 55
ответ: 55