1. Алгебра
  2. Найти все значения параметра

Найти все значения параметра , при которых уравнение имеет ровно два решения : sin(x² -7x +a) · cos(x²-x-a) + 2x² - 14x + 2a = 0

dimasikmirnyy9 dimasikmirnyy9    3   30.07.2021 04:07    3

Ответы
ученый2222 ученый2222  29.08.2021 05:29

(см. объяснение)

Объяснение:

\sin\left(x^2-7x+a\right)\cdot\cos\left(x^2-x-a\right)+2x^2-14x+2a=0

Перейдем от произведения тригонометрических функций к сумме:

\dfrac{1}{2}\cdot\left(\sin\left(2x^2-8x\right)+\sin\left(-6x+2a\right)\right)+2x^2-14x+2a=0

Преобразуем выражение, записанное выше:

\sin\left(2x^2-8x\right)-\sin\left(6x-2a\right)+4x^2-28x+4a=0\\\sin\left(2x^2-8x\right)+2\left(2x^2-8x\right)=\sin\left(6x-2a\right)+2\left(6x-2a\right)

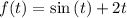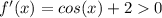Введем функцию f(t)=\sin\left(t\right)+2t. Она монотонно возрастает, так как f'(x)=cos(x)+20.

Тогда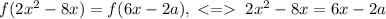 f(2x^2-8x)=f(6x-2a),\;\;2x^2-8x=6x-2a.

Продолжим решение:

2x^2-8x=6x-2a\\x^2-7x+a=0

Полученное уравнение имеет два корня, если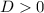 D0:

D=49-4a0,\;=\;a

Итого при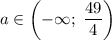 a\in\left(-\infty;\;\dfrac{49}{4}\right) исходное уравнение имеет ровно два различных решения.

Задание выполнено!

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
СофариПарк3 СофариПарк3  30.06.2019 19:40
Решить систему x-4y=3 x в квадрате -21y=28...
mishkateddi19 mishkateddi19  30.06.2019 19:40
Как решать систему уравнений сложения,подстановки,графическим...
Детство003 Детство003  30.06.2019 19:40
Пересекаются ли графики функций у=-2х+3 и у=-2х+7 у=3х-8 и у=2х+8 для пересекающихся графиков найти координаты точки пересечения...
kanevskiygabe kanevskiygabe  30.06.2019 19:40
Решите неравенство cos3x-cos2x меньше или равно 0...
maksim22441 maksim22441  30.06.2019 19:40
Как решить этот пример 9*(-1\18)+4=...
cehrjdfyflz1603 cehrjdfyflz1603  30.06.2019 19:40
Футболка стоит 220 рублей. сколько футболок можно будет купить на 1000 рублей в период распродажи, когда скидка на футболки составляет 20 процентов...
link21 link21  10.09.2020 10:20
корень0,7x^2-2x+3 =корень0, 7x^2+x-6...
kaspiridv603 kaspiridv603  10.09.2020 10:47
Решить систему уравнений подстановки 1.{x^2+y^2=17 {y-x+3=0 2. {x^2+y^2=8,5 {y-x+4=0...
marius95 marius95  01.04.2022 09:40
1. Розв яжіть квадратні рівняння за до формулі коренів a) 2x²² + 8x - 42=0б) 2x²² - 14x + 20=0....
Tustik777 Tustik777  01.04.2022 10:47
Винесіть множники з-під знака кореня 1) 5√3. 2)2а²√3а...

Популярные вопросы