1. Алгебра
  2. Найти соs(a), tg(a),ctg(a),если

Найти соs(a), tg(a),ctg(a),если sin(a)=2/3. 0

lykuanenkoartem lykuanenkoartem    1   21.05.2019 06:30    3

Ответы
muss07 muss07  15.06.2020 05:45

т.к. угол первой четверти то значения cosa,tga,ctga будут положительными.Найдём cosa из формулы.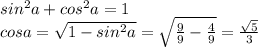sin^2a+cos^2a=1\\cosa=\sqrt{1-sin^2a}=\sqrt{\frac{9}{9}-\frac{4}{9}}=\frac{\sqrt{5}}{3}

1+tg^2a=\frac{1}{cos^2a}\\tga=\sqrt{(\frac{1}{\frac{\sqrt{5}}{3}})^2-1}=\sqrt{\frac{9}{5}-\frac{5}{5}}=\frac{2}{\sqrt{5}}\\ctga=\frac{1}{tga}=\frac{1}{\frac{2}{\sqrt{5}}}=\frac{\sqrt{5}}{2}

 

ПОКАЗАТЬ ОТВЕТЫ
ЛераКлаф ЛераКлаф  15.06.2020 05:45

(cosa)^2=1-(sina)^2

(cosa)^2=1-(2/3)^2=1-4/9=5/9

cosa=+или - корень из 5 /3

т.к. а принадлежит 1 четверти, то cosa= корень из 5 /3

 

 

 tga=sina/cosa=2/3: ( корень из 5 /3)=2/ корень из 5

ctga = 1/tga= корень из 5 / 2

 

 

 

 

 

 

 

 

 

 

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
ERKO20 ERKO20  20.12.2021 23:03
Построй график функции у=|х|.С графика выясни значение у,если х=-5...
Lol2288502 Lol2288502  20.12.2021 23:00
Реши неравенство и выбери правильный ответ...
прииииииип прииииииип  20.12.2021 22:53
... абсолютно не знаю что с этим делать, поставят 2 :...
Nikalusha Nikalusha  20.12.2021 22:53
16x(у квадраті)-1=0. Розв язати рівняння...
Arina2008egor Arina2008egor  20.12.2021 22:50
5корней из разобраться,как найти тут cos a и sin a если всего 1 аргумент,как это нормально расписать и как найти все 5 корней ? если подставлять k от 0 до 4 то какие детали,распишите...
zhaslanovd zhaslanovd  20.12.2021 22:49
Составь биквадратное уравнение, если известны его корни: x1,2 = ± 3, x3,4 = ± 1/5 x4 +x2 += 0. Назад Проверить...
Малефисента1111111 Малефисента1111111  20.12.2021 22:47
очень нужно сегодня успеть сдать до 23:59 я не успеваю , осень все что знаете от...
Русик271 Русик271  20.12.2021 22:41
Найдите значение выражения −3³+b²-1,5b при = −4. побыстрее...
aishaolzhas aishaolzhas  20.12.2021 22:38
Как изменить ребро куба чтобы его объем увеличился в m^3 раз...
nataliarianna29 nataliarianna29  20.12.2021 22:36
Упростите выражение:(a+5)(a-3)-(a-1)(a+3) . Найдите его значение, если a=-2,384....

Популярные вопросы