Найти производные следущих функций Подробно если можно

ответы есть но мне нужно решение я что-то в этом профан
1)-tg2x✓cos2x

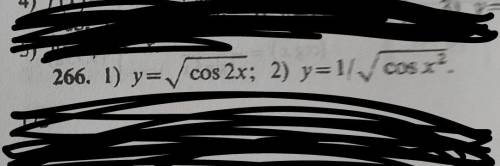
Найти производные следущих функций Подробно если можноответы есть но мне нужно решение я что-то в эт

Ответы

azhiltsova15ozb142 29.07.2021 16:54

Производную берем так же, как у обычных степенных функций: (х^а)' = а*х^(а-1),

НО функции сложные, нужно взять еще производные внутренних функций.

$y = \sqrt{ \cos(2x) } = ( \cos(2x)) {}^{ \frac{1}{2} }$

$y '= \frac{1}{2} {( \cos(2x)) }^{ - \frac{1}{2} } \times ( \cos(2x))' \times (2x)' = \\ = \frac{1}{2 \sqrt{ \cos(2x) } } \times ( - \sin(2x)) \times 2 = \\ = - \frac{ \sin(2x) }{ \sqrt{ \cos(2x) } } \times \frac{ \sqrt{ \cos(2x) } }{ \sqrt{ \cos(2x) } } = - \frac{ \sin(2x) \sqrt{ \cos(2x) } }{ \cos(2x) } = \\ = - tg(2x) \sqrt{ \cos(2x) }$

$y= \frac{1}{ \sqrt{ \cos( {x}^{2} ) } } = ( \cos( {x}^{2} ) ) {}^{ - \frac{1}{2} } \\$

$y '= - \frac{1}{2} (\cos( {x)}^{2} ) {}^{ \frac{3}{2} } \times ( \cos( {x}^{2}) ) ' \times ( {x}^{2} ) '= \\ = - \frac{1}{2 \sqrt{ \cos {}^{3} ( {x}^{2} ) } } \times ( - \sin( {x}^{2} ) ) \times (2x) = \\ = \frac{x \sin( {x}^{2} ) }{ \sqrt{ \cos {}^{3} ( {x}^{2} ) } } = \frac{x \sin( {x}^{2} ) }{ \cos( {x}^{2} ) \sqrt{ \cos( {x}^{2} ) } } = \frac{xtg( {x}^{2}) }{ \sqrt{ \cos( {x}^{2} ) } }$