1. Алгебра
  2. Найти производную функции: y=

Найти производную функции: y= 5x^4-1/x^3-x+2 найти производную функции: a) y=2sinx+3cosx б) y=4tgx-3cosx в) y=5sinx-ctgx г сделать как можно быстрее заранее всем кто !

ярик467 ярик467    3   01.03.2019 10:10    2

Ответы
Bordeaux Bordeaux  23.05.2020 18:07

y= \frac{5x^4-1}{x^3-x+2}\\y^`=(\frac{5x^4-1}{x^3-x+2})^`=\frac{(5x^4-1)^`\cdot(x^3-x+2)-(x^3-x+2)^`\cdot(5x^4-1)}{(x^3-x+2)^2}=\\ \frac{20x^3\cdot(x^3-x+2)-(3x^2-1)\cdot(5x^4-1)}{(x^3-x+2)^2}=\frac{20x^6-20x^4+40x^3-15x^6+3x^2+5x^4-1}{(x^3-x+2)^2}=\\ \frac{5x^6-5x^4+40x^3+3x^2-1}{(x^3-x+2)^2}

 

y=2sinx+3cosx\\y^`=(2sinx+3cosx)^`=(2sinx)^`+(3cosx)^`=2sinx-3sinx=-sinx

 

y=5sinx-ctg\\y^`=(5sinx-ctgx)^`=(5sinx)^`-(ctgx)^`=5cosx+\frac{1}{sin^2x}

 

y=11cosx-2tg\\y^`=(11cosx-2tgx)^`=(11cosx)^`-(2tgx)^`=-11sinx+\frac{2}{cos^2x} 

 

y=4tgx-3cosx\\y^`=(4tgx-3cosx)^`=(4tgx)^`-(3cosx)^`=4*\frac{1}{cos^2x}+3sinx=\\\frac{4}{cos^2x}+3sinx

 

ПОКАЗАТЬ ОТВЕТЫ
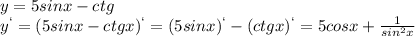
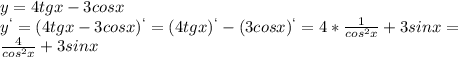
Другие вопросы по теме Алгебра
lainzord lainzord  14.03.2022 18:09
-2с³d⁴(8c²-c³d+4d³) =2x(x²+8x-3)=-0,3mn(2mn²-4m²n+3mn)=...
79025585606 79025585606  14.03.2022 18:07
18 учеников класса посещают кружок по математике, 16 по рисованию, двое учеников не один из кружков не посещают. Сколько учеников посещают кружок по математике и...
YaKuss YaKuss  14.03.2022 18:04
одна сторона прямоугольника на 1 см больше, а другая на 3 см меньше стороны квадрата. Найдите сторону квадрата, если его площадь больше площади прямоугольника на...
mockingbird12 mockingbird12  14.03.2022 18:04
Сколько разных слов можно образовать при перестановке букв слова Воссоединение ?...
Павел9641 Павел9641  14.03.2022 18:01
Привет с одним заданием, буду очень благодарен. Заранее . Построен полигон абсолютных частот попаданий дартсиста в мишень. График По данному полигону.1) Постройте...
123Никита5634 123Никита5634  14.03.2022 17:52
Алгебра 9 класс если cosa =1/9...
МашаКан МашаКан  14.03.2022 17:49
С объяснением ! Чему равен предел функции в точке (0;0)?...
спайки5 спайки5  31.08.2019 01:00
Выполните умножение (4x + 3)*(2x - 5)...
pidarok2281 pidarok2281  31.08.2019 01:00
Доказать sina+sinb+sing=4cos (a/2)cos (b/2)cos (g/2), где a - альфа, b - бета g - гамма углы треугольника...
darkilia2006p01bb5 darkilia2006p01bb5  31.08.2019 00:50
Преобразуйте в многочлен (а-6)(а+6)...

Популярные вопросы