С объяснением ! Чему равен предел функции 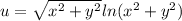 в точке (0;0)?
в точке (0;0)?
Другие вопросы по теме Алгебра
Популярные вопросы
- Впервые в нашей стране вопрос об ожидаемом числе детей был включен в программу...
3 - Демография в исследовании своего предмета — естественного воспроизводства...
1 - Зависимость специального коэффициента рождаемости от возрастной структуры...
1 - Роль обобщающего показателя смертности аналогичного суммарному коэффициенту...
3 - Укажите соответствие между понятиями и их содержанием юридическое население...
2 - Самосохранительное поведение - система действий и установок личности, направленных...
2 - Числом жителей на 1 кв. км территории измеряется плотность населения степень...
2 - Мысль о том, что для повышения рождаемости необходимо и достаточно лишь...
1 - К числу субъективных факторов рождаемости относится стремление родителей...
1 - По данным Всероссийской микропереписи населения 1994 г. среднее желаемое...
2
Объяснение:
1)
Введем переменную:
t = √ (x² + y²)
Тогда уравнение выглядит так:
u = t·ln(t)
Еще раз преобразуем функцию:
u = t / (1 / ln (t))
По правилу Лопиталя:
lim u = lim t' / lim (1/ln(t))'
Находим отношение производных:
t ' / [(1/t)·t'] = t
Таким образом, нам надо найти предел выражения
√ (x² + y²) при x и y стремящихся к нулю.
Очевидно, этот предел равен нулю.