Найти площадь фигуры, ограниченой линиями: y= корень x, y= (x-2)^2, y= 0. подробно с решением (не фотомач)
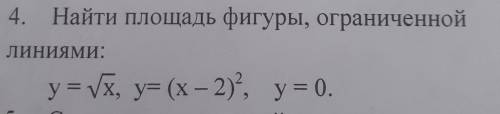
Другие вопросы по теме Алгебра
Популярные вопросы
- Як на кінцях ебонітової палички отримати одночасно два різнойменні заряди?...
2 - 1. З якими з наведених речовин реагуватиме соляна кислота: CaO, H2SO4,...
3 - Подумайте над питанням: Чи актуальна проблема вождя, порушена у поемі....
3 - 49:43 ПИТАННЯ: 711Розв яжи задачу. В поле для відповідь вводь тільки число...
3 - Зайди корінь рівняння округли його до сотих: 1) 19х=25 2) 7:х=57...
3 - Узнай и запиши, где и из чего получают сахар....
3 - Рівень 1 (кожне завдання оцінюється в ) 1. Укажіть формулу хімічного елемента,...
1 - Сделайте доклад описание озера...
1 - 1. У просторі дано чотирикутник АВСД та відомі координати його векторів...
3 - Після випаровування всієї води з 291 г насиченого при 60 С розчину одержали...
3
Точки пересечения , которые нам необходимы
Необходимая область делится на сумму двух криволинейных трапеций .
йц
Объяснение:
1333333333334444444444444444