1. Алгебра
  2. Найти площадь фигуры, ограниченной

Найти площадь фигуры, ограниченной линиями: y=3x^2+15x+30 и y=6-3x

111ВсЕзНаЙкА111 111ВсЕзНаЙкА111    3   09.06.2019 10:50    0

Ответы
inna755780987 inna755780987  08.07.2020 08:18
Для нахождения пределов интегрирования найдем точки пересечения параболы и прямой: 
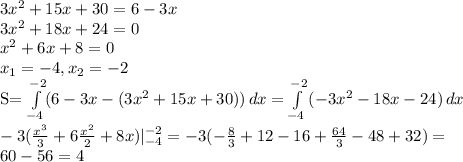
3 x^{2} +15x+30=6-3x \\ 3 x^{2} +18x+24=0 \\ x^{2}+6x+8=0 \\ x_{1} =-4, x_{2} =-2

S= \int\limits^{-2}_{-4}(6-3x-(3 x^{2} +15x+30)) \, dx = \int\limits^{-2}_{-4} {(-3 x^{2} -18x-24)} \, dx \\ -3( \frac{ x^{3} }{3} +6 \frac{ x^{2} }{2}+8x)| _{-4} ^{-2} =-3( -\frac{8}{3} +12-16+ \frac{64}{3} -48+32)= \\ 60-56=4
ПОКАЗАТЬ ОТВЕТЫ
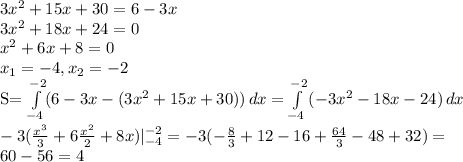
Другие вопросы по теме Алгебра
ренат123456789 ренат123456789  17.05.2019 20:13
700/(120-x)=-381 решите это уравнение...
black93 black93  17.05.2019 21:00
Пусть х1 и х2 – корни уравнения х2 – 18х -15 =0. не решая уравнение, вычислите : х2 : х1 + х1 : х2 +6....
ert12375 ert12375  17.05.2019 21:00
Производительности отца и сына относятся как 8: 4. сначала в течение трех часов они обрабатывали земельный участок вместе, затем отец устал и пошел отдыхать. сколько...
annajortsorensen annajortsorensen  17.05.2019 21:00
Как раскладывать на множители вот такие многочлены: a^ вообще не въезжаю,! p.s. ответ должен получится такой:...
azazaka220 azazaka220  17.05.2019 21:00
Решить . с подробным решением, ! 0,64 корень квадратный из (0,8 в степени х(х-3) ) 1...
murplushka murplushka  17.05.2019 20:08
Решите уравнение! n + s(n) = 1001 с подробным решением. кто все сделает, тому может отправлю рублей 50....
ТвойВраг ТвойВраг  17.05.2019 21:00
Кто с тригонометрией? нужен общий алгоритм для определения общих решений двух тригонометрич равенств, допустим sin7x = -1 v cos2x = -1, при подстановке возможных k...
nlimel nlimel  17.05.2019 21:00
Определите, при каком значении х: значение выражения 5 ( x-3) больше . 12 значения выражения 2x-7 на 2 6...
Graxx Graxx  17.05.2019 20:06
Что называется частотой случайного события? (кратко)...
хех60 хех60  17.05.2019 21:00
[0; п], имеетуравнение cos6x+cos4x=0 ?...

Популярные вопросы