Найти наибольшее и наименьшее значение функции напишите подробный ответ.
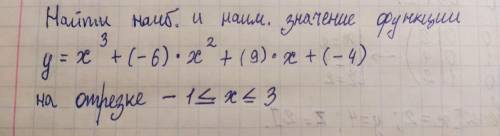
Другие вопросы по теме Алгебра
Популярные вопросы
- Участок земли имеет форму прямоугольника длина которого 50 м а...
1 - 1) что такое почва 2) свойство почвы 3) виды почвы 4) запах почвы...
2 - На книжной полке расположены 6 томов. вероятность того. что том...
3 - Динозавры относились к наземным рептилиям. среди них встречались...
3 - Вначале запишите сумму в виде произведения, а затем вычислите....
3 - Вевропейских колониях создавалось общество свободное или рабов?...
3 - На 6 халатов пошло 24 метров ткани еще нужно сшить 9 таких халатов...
1 - Составьте формулы солей образованных следующими катионами и анионами:...
3 - 1мастер может выполнить работу за 12 дней а 2 мастер ту же работу...
2 - Лебедь, рак и щука в известной басне крылова тянут воз с одинаковыми...
1
y = x³ - 6x² + 9x - 4
Найдём производную :
y' = (x³ - 6x² + 9x - 4)' = (x³)' - 6(x²)' + 9(x)' - 4' = 3x² - 12x + 9
Приравняем производную к нулю, найдём критические точки :
3x² - 12x + 9 = 0
x² - 4x + 3= 0
По теореме Виета :
x₁ = 1 x₂ = 3
Обе точки принадлежат заданному отрезку .
Найдём значения функции в критических точках и на концах отрезка и сравним их :
y(1) = 1³ - 6 * 1² + 9 * 1 - 4 = 1 - 6 + 9 - 4 = 0
y(3) = 3³ - 6 * 3² + 9 * 3 - 4 = 27 - 6 * 9 + 27 - 4 = 54 - 54 - 4 = -4
y(-1) = (- 1)³ - 6 * (- 1)² + 9 * (- 1) - 4 = - 1 - 6 - 9 - 4 = - 20
ответ : наибольшее значение функции равно 0 , а наименьшее значение равно ( - 20) .