1. Алгебра
  2. Найти |a+b|, если a=25/a-b

Найти |a+b|, если a=25/a-b и b=144/b-a

Tolganay11 Tolganay11    2   02.01.2022 15:11    2

Ответы
Алия0051 Алия0051  02.01.2022 15:20

Из каждого равенства выразим сумму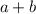 a+b:

a=\dfrac{25}{a} -b \Rightarrow a+b=\dfrac{25}{a}

b=\dfrac{144}{b} -a \Rightarrow a+b=\dfrac{144}{b}

Приравняем правые части полученных соотношений:

\dfrac{25}{a}=\dfrac{144}{b}

a=\dfrac{25}{144}b

Подставим это соотношение в одно из выражений для суммы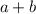 a+b:

a+b=\dfrac{144}{b}

\dfrac{25}{144}b+b=\dfrac{144}{b}

\dfrac{169}{144}b=\dfrac{144}{b}

b^2=144:\dfrac{169}{144}

b^2=\dfrac{144^2}{169}

Возможны два случая:

b_1=\dfrac{144}{13}\Rightarrow a_1=\dfrac{25}{144}\cdot \dfrac{144}{13}=\dfrac{25}{13}

b_2=-\dfrac{144}{13}\Rightarrow a_2=\dfrac{25}{144}\cdot\left(- \dfrac{144}{13}\right)=-\dfrac{25}{13}

Однако оба случая приводят к одному и тому же итоговому ответу:

|a+b|=\left|\pm\left(\dfrac{144}{13}+\dfrac{25}{13} \right)\right|=\left|\pm\dfrac{169}{13} \right|=\left|\pm13\right|=13

ответ: 13

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
AMINA2007133456 AMINA2007133456  12.06.2019 21:10
Решите уравнение (4х-15)(5х+35)(0.75-0.2х)=0...
Ангелина22325 Ангелина22325  12.06.2019 21:10
Найти число целых значений параметра a, при которых уравнение не имеет корней...
Poli2533 Poli2533  12.06.2019 21:10
Значение функции у=2х^2 равно 1)8 2)55 найдите соответствующие ему значения аргумента...
спартак37 спартак37  12.06.2019 21:10
Решите уравнение! 3tg^2 x-8=4cos^2 x...
Chokoladik Chokoladik  12.06.2019 21:10
Напишите формулу функции, график которой параллелен оси абсцисс...
ilham11997766 ilham11997766  12.06.2019 21:10
Яв упор не помню,как складывают квадратные корни(( сложить: корень из трех+корень из двух, корень из двух+ один(без корня), корень из ста+корень из девяносто девяти...
isackanova isackanova  12.06.2019 21:10
Выражение и вычислите его значение при а=-1/3 2(0.3a-1)-2/3(3a-5) ! всем...
0123220210 0123220210  12.06.2019 21:10
Подскажите как решить такое неравенство: -3х+6 0...
irinslab irinslab  12.06.2019 21:10
Укажите наибольшее число, принадлежащее промежутку [5; 7)...
Litsonchik Litsonchik  22.05.2019 00:30
Найти производную функции y=x^12+sinx...

Популярные вопросы