Найдите значение выражения 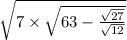
используя свойства корней
Другие вопросы по теме Алгебра
Популярные вопросы
- Приведите пример познавательной функции литературы...
1 - Чему равно наибольшее значение дроби с 20 заданием...
2 - До ть будь ласка! 28 3/4 - 7/12=...
3 - автомобиль ехал 3 часа со скоростью 62 км ч а затем 2 ч со скоростью 15 км ч...
1 - Айдар и Айсар идут по дороге, которая завела их в туман. Сможет ли Айсар в тумане...
2 - Почему Беларусь занимает более компактную территорию чем Португалия Чехия Австрия...
2 - написание согласной буквы с в корне слова может проверить 1) просить...
1 - 23 мл = ? л; 275мм в квадраті = ? м в квадраті...
3 - Дискриминантом надо решить ...
2 - надо найти с теоремы пифагора) Только с объяснениями т.к. я дурaчок...
2
Объяснение:
=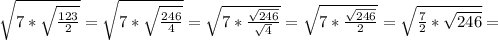
=![\sqrt{\sqrt{(\frac{7}{2})^2*246}} =\sqrt[4]{\frac{49}{4}*246} = \sqrt[4]{\frac{6027}{2}}](/tpl/images/1357/1388/66011.png)