Найдите значение выражение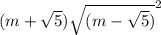
при m=2,2
решение и ответ ​

Чтобы найти значение выражения, нужно подставить значение m=2,2 вместо каждой переменной m внутри выражения и выполнить все арифметические операции по очереди.

Исходное выражение:

(m + √5) √(m - √5)^2

Подставляем m=2,2:

(2,2 + √5) √(2,2 - √5)^2

Выражение ((минус корень из пяти) возвести в квадрат) означает, что сначала нужно вычислить значение выражения внутри корня, а затем возвести его в квадрат.

Выражение (2,2 - √5) можно упростить:

2,2 - √5 ≈ 0,6495 (округленно до 4 знаков после запятой)

Теперь возьмем корень (из 0,6495) и возведем его в квадрат:

√0,6495 ≈ 0,8059 (округленно до 4 знаков после запятой)

0,8059^2 ≈ 0,6495 (округленно до 4 знаков после запятой)

Итак, мы получили значения под выражением √(m - √5)^2:

0,6495

Теперь подставим все значения в исходное выражение:

(2,2 + √5) * 0,6495

Теперь нужно вычислить значение (2,2 + √5):

2,2 + √5 ≈ 4,413 (округленно до 3 знаков после запятой)

Итак, мы получаем:

4,413 * 0,6495

Выполняем эту операцию:

4,413 * 0,6495 ≈ 2,858 (округленно до 3 знаков после запятой)

Таким образом, значение выражения при m=2,2 равно примерно 2,858.