Найдите сумму бесконечной прогрессии (bn), если q > 0, b3 = 3/8 a b1 = 3/2?
Другие вопросы по теме Алгебра
Популярные вопросы
- Функция задана формулой у=4/х. Заполните таблицу, вычислив соответствующее значение...
3 - V=y^√x+4y u=(tgx)^sinyz Решите даю...
1 - Діагоналі ромба розбивають його на 4 трикутники знайти кути якщо один з кутів...
2 - какой главный приём в стихотворении Ещё майская ночь...
1 - Поясніть яку роль у формуванні клітинної мембрани відіграють білки,жири та вуглеводи...
1 - Бумага и чернила На письменном столе стопкой лежали одинаковые листы чистой...
1 - Вибери з множини у = {118; 210; 518; 625; 836; 940} числа, які є кратними: а)...
2 - С графика найдите значение x, соответствующее y, равному -2.1)-12)13)-24)0...
3 - Постройте график функции У= 2х -3...
1 - Поставьте глагол в форму инфинитива. Model−−−−−: He didn\ t want tobeasked that...
2
По формуле найдем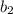 :
:
Все подставляем и получаем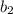 =
= 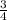
Теперь подставляем все в эту формулу:
q=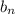 :
: 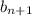
Получаем q=0,5
Теперь нужна вот такая формула:
S=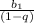
Все подставим и получим сумму бесконечной геометрической прогрессии S=3
ответ: 3
__________
Нужно формулы выучить :3
b₂²=b₁*b₃=3/2*3/8=9/16;
1)-3/4; qₓ=b₂/b₁=-3/4:3/2=-1/2;∅ в условии q > 0
2)b₂=3/4; qₐ=b₂/b₁=3/4:3/2=1/2;
Sₐ=b₁/(1-qₐ)=3/2:(1/2)=3;