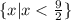1. Алгебра
  2. Найдите область определения

Найдите область определения
y=lg(3^2-2x)

MrVyacheslav228 MrVyacheslav228    2   31.10.2019 13:33    0

Ответы
kopalkina02 kopalkina02  10.10.2020 10:29

ответ: Запись в виде интервала: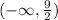 (-\infty, \frac{9}{2})

Нотация построения множества: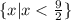 \{ x|x < \frac{9}{2} \}

Объяснение: Положим аргумент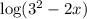 \log (3^2-2x) больше 0, чтобы выяснить, где определено данное выражение.

3^2-2x0

Решим относительно x.

Возведем 3 в степень 2.

9-2x0

Вычтем 9 из обеих частей неравенства.

-2x-9

Разделим каждый член на -2 и упростим.

Разделим каждый член в выражении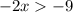 -2x-9 на -2. При умножении или делении обеих частей неравенства на отрицательное значение, знак неравенства меняется на противоположный.

\frac{-2x}{-2}

Сократим общий множитель -2.

x

Деление двух отрицательных значений дает положительный результат.

x

Решение включает все истинные интервалы.

x

Областью определения являются все значения x, которые делают выражение определенным.

Запись в виде интервала: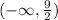 (-\infty, \frac{9}{2})

Нотация построения множества: \{ x|x < \frac{9}{2} \}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
kushtueva kushtueva  14.04.2020 13:15
Постройте график функции у=2х-5...
khabarovanastya khabarovanastya  14.04.2020 13:15
Визнач, чи буде пара чисел (6;-9) розв язком рівняння 5x+2y−12=0 ? Відповідь:пара чисел (6;-9) а) є розв’язком рівняння б) не є розв’язком рівняння 5x+2y−12=0​...
boldarev2001 boldarev2001  14.04.2020 13:15
Найдите наименьшее значение n , при котором n! делится на 1400...
sweetk sweetk  14.04.2020 13:15
РЕБЯТ ОЧЕНЬ Преобразуйте заданные пары алгебраических дробей так, чтобы получились дроби с одинаковыми знаменателями: 1) 5/a и 7/a-b 2)b/a+b и b/a 3)14/a и 3/a-1...
Егор4ik18 Егор4ik18  26.05.2020 14:21
Найти координаты фокуса и написать уравнение директрисы для параболы...
matema2 matema2  26.05.2020 14:21
Найти производную функции ​...
alice1607 alice1607  27.05.2020 21:18
Найдите значение х при котором разность значений выражений 7-х х 5 и х 4-х равна 14...
murat121221 murat121221  27.05.2020 21:19
СТАВЛЮ Знайдіть суму і різницю многочленів 4x^3^+3x^2^+x-4 і 2x^3^-x^2^+2x+7 Числа в знаку ^ означають степень...
yaltalove67 yaltalove67  27.05.2020 21:19
№ 5 Закончите разложение на множители: a) m2 - n2 + 9m + 9n =¿ - n2 ¿ + (9m + 9n) = (m – n) ( m+ n) + 9 (m + n) = … б) a2 - b2 – 5a – 5b = ¿ - b2¿ – (5a + 5b) = …...
elena0795 elena0795  27.05.2020 21:19
Найдите угловой коэффициент касательной к графику функции y=2x³- 6x+5 x0=1?...

Популярные вопросы