1. Алгебра
  2. Найди значение выражения

Найди значение выражения 4+cos2β. Если cosβ=0,4. ответ округли до сотых.

adadurovf adadurovf    3   17.08.2020 13:40    15

Ответы
cmpunk559 cmpunk559  15.10.2020 16:00

Косинус двойного аргумента:

\cos 2x=\cos^2x-\sin^2x

Если выразить из основного тригонометрического тождества квадрат синуса \sin^2x=1-\cos ^2x и подставить в данную формулу, то получится еще одна формула косинуса двойного угла:

\cos 2x=\cos^2x-(1-\cos^2x)=\cos^2x-1+\cos^2x=2\cos^2x-1

Аналогично, можно вывести еще одну формулу:

\cos 2x=(1-\sin^2x)-\sin^2x=1-\sin^2x-\sin^2x=1-2\sin^2x

В данном случае удобно использовать формулу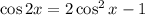 \cos 2x=2\cos^2x-1, так как найти косинус двойного аргумента нужно, зная только косинус одинарного аргумента.

Преобразуем выражение, используя формулу косинуса двойного аргумента:

4+\cos2\beta =4+2\cos^2\beta-1=3+2\cos^2\beta=

=3+2\cdot0.4^2=3+2\cdot0.16=3+0.32=3.32

ответ: 3.32

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
AleksaKiki AleksaKiki  18.07.2019 10:00
Найдите tg a,если известно, что cos a=2дробь корень5,0...
ксю825 ксю825  18.07.2019 10:00
Решите систему уравнений х^2 + у^2 = 5, х + у = 3...
ciel13891 ciel13891  18.07.2019 10:00
За 3 дня в колхозе вскопали 250га. площадь, вспаханная в первый день, составляет 90℅ от площади второго дня, а площадь вспаханная в третий день, составляет 1\3 от площади первого...
AdelinaArMi AdelinaArMi  18.07.2019 10:00
Найдите пересечение промежутков,заданных неравенствами |x| меньше или равен 5 и -7 меньше или равен x меньше или равен 1...
Максим5955 Максим5955  18.07.2019 10:00
Дано: (bn)- прогрессия b5= -1/8 ; q=2√2 найти: b7 ,(понятное решение)...
alina1930 alina1930  18.07.2019 10:00
20б! решите: sin²x+sin²2x+sin²3x=1,5...
Beauty52 Beauty52  18.07.2019 10:00
Постройте график функции: у=(2-х)(х-6)...
Zarishka1312 Zarishka1312  18.07.2019 10:00
Часы на старой башне и часы на камине бьют одновременно и пробили 19 раз. определить час, который они показывали, зная, что часы на башне отстают от часов на камине на 2 секунды и...
prve17 prve17  18.07.2019 10:00
Три четвертых все это в 8степени умножить на четыре третьих и все это в седьмой степени надо сравнить с минус 0,75 в нулевой степени...
Fukci Fukci  18.07.2019 10:00
Розкладіть на множники двочлен 125-z3( в кубі)...

Популярные вопросы