20б! решите: sin²x+sin²2x+sin²3x=1,5
Ответы
Пользуемся формулой понижения степени:
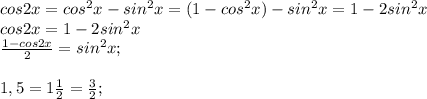
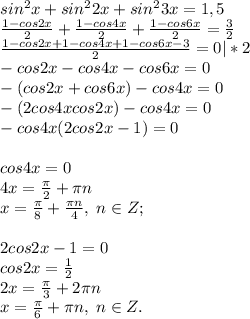
ПОКАЗАТЬ ОТВЕТЫ
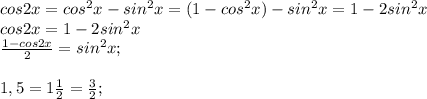
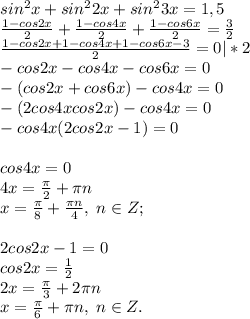
Другие вопросы по теме Алгебра
Популярные вопросы
- На каком расстоянии следует поместить заряды по 4*10 в -7 степени...
2 - Составить формулы солей, гидроксидов, кислот и оксидов для бария,...
2 - Если положить на стол брусок, он будет покоиться, а шар обычно катится...
1 - Длина окружности c=12,56 см. вычисли диаметр и радиус этой окружности....
2 - Отгадайте загадку «два братца через дорогу живут...
2 - Если положить на стол брусок, он будет покоиться, а шар обычно катится...
2 - Напишите все изомеры с10н14,заранее большое )...
3 - Два угла со взаимно перпендикулярными сторонами относятся как 4...
1 - Найдите точки пересечения графика линейных уровнений; функции y=3x+4;...
3 - Jacks first lesson starts jacks first lesson starts jack hasjacks...
2