Навстречу друг другу из двух городов, расстояние между которыми составляет 204 км, одновременно выехали два мотоциклиста. Скорость первого мотоциклиста составляет 55 км/ч, а скорость второго мотоциклиста равна 27 км/ч. Первый мотоциклист, проехав некоторую часть пути, сделал остановку на 16 минут, а затем поехал дальше до встречи со вторым мотоциклистом. Найдите расстояние от города, из которого выехал первый мотоциклист, до места встречи со вторым мотоциклистом.
Другие вопросы по теме Алгебра
Популярные вопросы
- Каким прибором измеряем атмосферное давление...
3 - Напишите небольшое сочинение на тему: интересна ли современному...
2 - Как назывался церковный суд для преследования ереси? 1)информатизация...
1 - Решите плз, надо сейчас, умоляю. a) (5x^2+y^2)^2= б) (-3a^5+2,5b)^2=...
1 - _ca+_h3po4→_ca3(po4)2+_h2 рставьте коэффиценты...
1 - Вясный солнечный день требуеться изменить высоту ав дерева ....
1 - Придумать по 1 предложению с каждым словом: at night, at 3 o...
3 - Придумать загадку про свой любимый молочный продукт...
2 - Представьте в виде десятичной или периодической дроби числа:...
3 - Представь числа 60 40 99 суммы двух круглых чисел...
2
Пусть t час - время в пути второго
Тогда первый находился в движении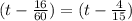 час
час
Второй проехал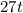 км, а второй проехал
км, а второй проехал  час
час
Так как по условию они встретились, значит проехали вместе весь путь.
Уравнение:
За это время второй проехал
а первый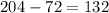 км
км
О т в е т. расстояние от города, из которого выехал первый мотоциклист, до места встречи со вторым мотоциклистом равно 132 км