Люди добрые

/

Алгебра 10 класс
1 задание-угловой коэф равен значение производной в фиксир точке
Фиксир точка Х0

Люди добрые /Алгебра 10 класс1 задание-угловой коэф равен значение производной в фиксир точкеФиксир

Ответы

Xidirova04 11.06.2021 07:20

Объяснение:

$f(x)=\frac{1}{2} *x^2+3x+2\ \ \ \ \ x_0=1\\y'(x)=(\frac{1}{2} *x^2+3x+2)'=x+3.\ \ \ \ \Rightarrow\\y'(1)=1+3=4.$

ответ: y'(1)=4.

$y=\frac{2x+3}{x^2-1} \ \ \ \ x_0=2.\\y_k=y(x_0)+y'(x_0)*(x-x_0)\\y(2)=\frac{2*2+3}{2^2-1} =\frac{7}{3}.\\y'(x_0)=(\frac{2x+3}{x^2-1})'=\frac{2*(x^2-1)-(2x+3)*2x}{(x^2-1)^2}=\frac{2x^2-2-4x^2-6x}{(x^2-1)^2}=\frac{-2x^2-6x-2}{(x^2-1)^2} =\frac{-2*(x^2+3x+1)}{(x^2-1)^2} .\\y'(2)=\frac{-2*(2^2+3*2+1)}{(2^2-1)^2} =\frac{-2*(4+6+1)}{(4-1)^2} =-\frac{2*11}{3^2}=-\frac{22}{9}.\\$ $y_k=\frac{7}{3}-\frac{22}{9}*(x-2)=\frac{7*3-22*(x-2)}{9}=\frac{21-22x+44}{9} =\frac{65-22x}{9}=\frac{65}{9}-\frac{22}{9}x .$

$a)\ y=3x^2-6x+1\\y'=(3x^2-6x+1)'=6x-6=0\\6x-6=0\\6x=6\ |:6\\x=1.\ \ \ \ \Rightarrow\\$

В окрестности точки x = 1 производная функции меняет знак с (-) на (+). Следовательно, точка x = 1 - точка минимума.

При х∈(-∞;1) функция убывает.

При х∈(1;+∞) фунуция возрастает .

$b)\ y=x^9-9x\\y'=(x^9-9x)'=9x^8-9=9*(x^8-1)=0\\9*(x^8-1)=0\ |:9\\x^8-1=0\\x^8=1\\x=\sqrt[8]{1}\\x_1=-1\ \ \ \ x_2=1$

В окрестности точки x = -1 производная функции меняет знак с (+) на (-). Следовательно, точка x = -1 - точка максимума.

При х∈(-∞;-1) фунуция возрастает .

В окрестности точки x = 1 производная функции меняет знак с (-) на (+). Следовательно, точка x = 1 - точка минимума.

При х∈(1;+∞) функция возрастает. ⇒

При х∈(-1;1) функция убывает.

ПОКАЗАТЬ ОТВЕТЫ

aleksa604 11.06.2021 07:20

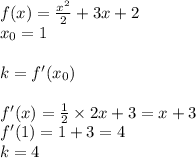
$f(x) = \frac{ {x}^{2} }{2} + 3x + 2 \\ x_0 = 1 \\ \\ k = f'(x_0) \\ \\ f'(x) = \frac{1}{2} \times 2x + 3 = x + 3 \\ f'(1) = 1 + 3 = 4 \\ k = 4$

$y = \frac{2x + 3}{ {x}^{2} - 1 } \\ x_0 = 2$

f(x) = y(x_0) + y'(x_0)(x - x_0)

$y(2) = \frac{4 + 3}{4 - 1} = \frac{7}{3} \\$

$y' = \frac{(2x + 3)'( {x}^{2} - 1) - ( {x}^{2} - 1)'(2x + 3)}{ {( {x}^{2} - 1 }^{2} } = \\ = \frac{2(x {}^{2} - 1) - 2x(2x + 3)}{ {( {x}^{2} - 1)}^{2} } = \frac{2 {x}^{2} - 2 - 4 {x}^{2} - 6x}{ {( {x}^{2} - 1)}^{2} } = \\ = \frac{ - 2 {x}^{2} - 6x - 2}{ {( {x}^{2} - 1)}^{2} } = - \frac{2( {x}^{2} + 3x + 1) }{ {( {x}^{2} - 1)}^{2} }$

$y'(2) = - \frac{2(4 + 6 + 1)}{(4 - 1) {}^{2} } = - \frac{2 \times 11}{9} = - \frac{22}{9} \\$

$f(x) = \frac{7}{3} - \frac{22}{9}(x - 2) = \frac{7}{3} - \frac{22x}{9} + \frac{44}{9} = \\ = - \frac{22x}{9} + \frac{44 + 21}{9} \\ f(x) = - \frac{22}{9} x + \frac{65}{9}$

- уравнение касательной

а)

$y = 3 {x}^{2} - 6x + 1 \\ y' = 6x - 6 \\ \\ 6x - 6 = 0 \\ x = 1 \\ - \: \: \: \: \: \: \: \: + \\ - - 1 - -$

Функция возрастает на (1; + беск)

Функция убывает на (- беск; 1)

б)

$y = {x}^{9} - 9x \\ y' = 9 {x}^{8} - 9 \\ \\ 9 {x}^{8} - 9 = 0 \\ {x}^{8} = 1 \\ x = \pm1 \\ + \: \: \: \: \: \: \: \: - \: \: \: \: \: \: + \\ - - ( - 1) - -1 - -$

Функция возрастает на (- беск; -1)U(1; + беск)

Функция убывает на (-1; 1)

а)

$f(x) = {x}^{3} - 9x \\ f'(x) = 0 \\ f'(x) = 3 {x}^{2} - 9 \\ 3 {x}^{2} - 9 = 0 \\ {x}^{2} = 3 \\ x = \pm \sqrt{3}$

б)

$f(x) = - \frac{2}{x} \\ f'(x) = - 2 \times ( - 1) {x}^{ - 2} = \frac{2}{ {x}^{2} } \\ \\ \frac{2}{ {x}^{2} } = 0 \\ x\ne0$

Нет критических точек

$f(x) = \frac{ {x}^{3} }{3} - \frac{5 {x}^{2} }{2} + 4x - 1 \\ f'(x) = {x}^{2} - 5x + 4 \\ \\ {x}^{2} - 5x + 4 = 0 \\ D= 25 - 16 = 9 \\ x_1 = \frac{5 + 3}{2} = 4 \\ x_2 = 1 \\ + \: \: \: \: - \: \: \: \: \: \: \: \: + \\ - -1 - - 4 - -$

ответ: 1 - точка максимума; 4 - точка минимума

$f(x) = \frac{2}{x} + 3x \\ f'(x) = - 2 {x}^{ - 2} + 3 = - \frac{2}{ {x}^{2} } + 3 \\ \\ - \frac{2}{ {x}^{2} } + 3 = 0 \\ \frac{ - 2 + 3 {x}^{2} }{ {x}^{2} } = 0 \\ 3 {x}^{2} - 2 = 0 \\ x = \pm \sqrt{ \frac{2}{3} } \\ x\ne0 \\ + \: \: \: \: \: \: \: \: \: \: \: \: \: - \: \: \: \: \: \: \: \: \: \: \: - \: \: \: \: \: \: \: \: \: \: \: + \\ - -( - \sqrt{ \frac{2}{3} } ) - - 0 - - \sqrt{ \frac{2}{3} } - -$

- корень из (2/3) - точка максимума

корень из (2/3) - точка минимума

Число - корень из(2/3) не входит в промежуток

[0,5; 3]

$f(0.5) = 4 + 1.5 = 5.5 \\ f( \sqrt{ \frac{2}{3} }) = 2 \times \sqrt{ \frac{3}{2} } + 3 \times \sqrt{ \frac{2}{3} } = \\ = \sqrt{6} + \sqrt{6} = 2 \sqrt{6} \\ f(3) = \frac{2}{3} + 9 = 9 \frac{2}{3}$