Log5(3x+1)<2 система линейных уравнений.

или .

Объяснение:

Дано неравенство:

По свойству логарифма, мы знаем, что аргумент логарифма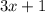 всегда должен быть больше нуля. Поэтому найдём область допустимых значений неравенства:

Теперь найдем множество решений нашего неравенства в виде системы с областью допустимых значений. Представим число 2 как логарифм с аргументом 5 по основанию 5:

Для выражения при 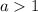равно 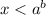, поэтому наше неравенство имеем право представить в виде:

Преобразуем:

Исходя из области допустимых значений и множества решений самого неравенства, получаем пересечение: или .