Каноническое уравнение эллипса , если две его вершины находятся в точках а1 (-8; 0) и а (8; 0) , а фокусы имеют координаты (плюс-минус 5; 0)
Ответы
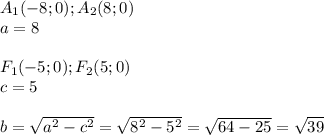
 - каноническое уравнение эллипса
- каноническое уравнение эллипса
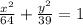 - искомое уравнение эллипса
- искомое уравнение эллипса
Другие вопросы по теме Алгебра
Популярные вопросы
- Втреугольнике abc стороны ac и ab равны. из точки f, лежащей на стороне ac на...
1 - Какая обязанность граждан и почему прописывается ч.3 ст.44 конституции рф?...
1 - Знайді кут b трикутника авс , якщо ас=37см , ав=7, вс=33...
1 - Техника безопасности при работе с олифой? ...
3 - Примеры реализации прав жителями вашего региона...
2 - За нить прикрепленную к телу,потянули со силой 10 н в первый раз 2 с,а во второй...
2 - 8класс. 30 постройте график функции y= 7/ модуль x...
1 - Проанализируйте какие возможности россиянам права провозглашенные в конституции...
1 - Удача и не удача героев в произведение кавказ...
3 - Нужно написать отзыв (мини-сочинение, на 2 листа полных тетрадных_) о прочитанном...
1