1. Алгебра
  2. Какова множество всех возможных

Какова множество всех возможных значений выражений x/|x|-y/|y|-xy/|xy|

oleg120906 oleg120906    3   29.11.2021 10:37    3

Ответы
ПотнаяБабка2000 ПотнаяБабка2000  05.01.2022 17:00

\dfrac{x}{|x|}-\dfrac{y}{|y|}-\dfrac{xy}{|xy|}

В самом начале отметим, что область допустимых значений этого выражения: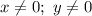 x\neq 0;\ y\neq 0.

Раскроем модуль:

1) x0;\ y0

\dfrac{x}{|x|}-\dfrac{y}{|y|}-\dfrac{xy}{|xy|}=\dfrac{x}{x}-\dfrac{y}{y}-\dfrac{xy}{xy}=1-1-1=-1

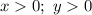
2) x0

\dfrac{x}{|x|}-\dfrac{y}{|y|}-\dfrac{xy}{|xy|}=\dfrac{x}{-x}-\dfrac{y}{y}-\dfrac{xy}{(-x)\cdot y}=-1-1-(-1)=-1

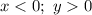
3) x

\dfrac{x}{|x|}-\dfrac{y}{|y|}-\dfrac{xy}{|xy|}=\dfrac{x}{-x}-\dfrac{y}{-y}-\dfrac{xy}{(-x)\cdot (-y)}=-1-(-1)-1=-1

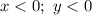
4) x0;\ y

\dfrac{x}{|x|}-\dfrac{y}{|y|}-\dfrac{xy}{|xy|}=\dfrac{x}{x}-\dfrac{y}{-y}-\dfrac{xy}{x\cdot(-y)}=1-(-1)-(-1)=3

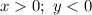
Таким образом, множество всех возможных значений выражений:

M=\{-1;\ 3\}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Нэтэли11 Нэтэли11  15.03.2020 02:40
Запишіть три перших члени числової послідовності, що задана формулою Cn=3n2(в квадраті)-2n​...
langueva1405 langueva1405  15.03.2020 02:38
решить с 1.1 по 1.12 и скажите автор учебника по ДПА математики ​...
Seagate0012 Seagate0012  15.03.2020 02:38
У выражение: cos (/4+)cos(/4−) +1/2()^2...
Natalia10000 Natalia10000  15.03.2020 02:36
РЕШИТЕ С УРАВНЕНИЯ:Бак наполняется двумя кранами за 6 часов одновременно. За какое время каждый кран в отдельности может наполнить бак,если известно, что первый кран...
Nagoshkaa Nagoshkaa  15.03.2020 02:34
Запишіть три перших члени геометричної прогресії, у якої b1 =3 q=2.​...
ValeriaChernysheva ValeriaChernysheva  15.03.2020 02:28
Найдите сумму первых шестнадцати членов арифметической прогрессии, в которой а) а1= 6,d=4 б)а1= 12, d=-3...
150029 150029  15.03.2020 02:28
решите номер 3 И если не сложно то номер 4 тоже решите...
DashaLOVE04 DashaLOVE04  06.04.2021 11:21
Геометрична прогресіяЗнайти q якщо b = 10; h = 0,1.​...
Aloha44 Aloha44  06.04.2021 11:21
Спростити вираз (b+3) (b-3)...
VikaSh86 VikaSh86  06.04.2021 11:21
Найти походную функции y=x-1/x+1+x+1/x-1...

Популярные вопросы