Какое условие необходимо потребовать для нахождения максимальной суммы квадратов двух рахличных корней? "При каких a сумма квадратов двух различных корней максимальна?"
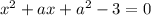
Другие вопросы по теме Алгебра
Популярные вопросы
- из точки о лежащей вне двух параллельных плоскостей а(альфа) и в(бета)...
1 - сделать синтаксический разбор 1. Свет на экран падал от масляной лампы,...
1 - Радианная мера одного из углов ромба равна 0,7п Найдите радианные меры...
3 - Занимала ли коммунистическая партия ведущее положение? Если да, то...
2 - (UJabан үзінді) Сонда да бір батыр жоқ Баяндай тап.Ер Баян алып қайтқан...
3 - 3. Выпишите из 3-го абзаца словосочетания «прилагательное + су- ществительное»....
1 - максимально сильно сжать изложение ...
1 - Опыт страховой компании показывает, что страховой случай приходится...
2 - Расскажите согласно определению абсолютной монархии, ее проявления...
1 - 6. Определи порядок действий. Вычисли, записывая действия столбиком.124...
2
-3/8.
Объяснение:
1) x²-4ax+5a=0
Если х1 и х2 - корни уравнения, то по теореме Виета
х1 + х2 = 4а и х1•х2 = 5а.
2) Сумма квадратов двух корней уравнения
(х1)^2 + (х2)^2 =(х1 + х2)^2 - 2•х1•х2 = (4а)^2 - 2•5а = 16а^2 -10а.
По условию эта сумма равна 6, тогда
16а^2 -10а = 6
16а^2 -10а - 6 = 0
8а^2 - 5а - 3 = 0
D = 25 -4•8•(-3) = 25 + 96 = 121
a =(5±11):16
a1 = 1
a2 = -6:16 = -3/8
3) Проверим, что при найденных значениях уравнение имеет два различных действительных корня.
✓При а=1 уравнение примет вид x²-4x+5=0. Дискриминант отрицательный, уравнение корней не имеет.
✓При а= -3/8 уравнение примет вид
x^2 -4•(-3/8)x+5•(-3/8)=0
х^2 +3/2•х - 15/8 = 0
8х^2 + 12х - 15 = 0
D =144 + 4•8•15 = 144+480=624>0, уравнение имеет два различных корня
ответ: -3/8.