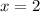Какое наименьшее значение и при каком значении переменной принимает выражение
х2 – 4х – 5?
Другие вопросы по теме Алгебра
Популярные вопросы
- Разгадай кроссворд по горизонтали 1 сумма чисел 999 и 1 по вертикали...
2 - Закончи записи . 1 дм2 больше ,чем 1 см2 в ? раз. 1 м2 больше...
2 - В500мл воды растворили 49 серноц кислоты вычеслите молярную концентрацию...
3 - Как нашествие батая на руси повлеяло на страны...
1 - Как растения могут при к регулярному вытаптыванию? примеры таких...
2 - Найдите значение переменной у, при котором сумма дробей 3у+9/3у-1...
2 - Переведите , ,текст. его название to be the first one. вот текст...
1 - От-ел об-ел по-ел с-ел образоват новие слава приставками...
2 - Ниже представлено письмо, написанное с фронта. в письме есть...
3 - Рассказ короткий про открытие антарктиды беллинсгаузеном и лазаревым....
1
Відповідь:
Пояснення:
Выражение принимает наименьшее значение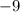 при
при 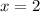
Объяснение:
Воспользуемся методом выделения полного квадрата:
Квадрат любого числа - число неотрицательное
Причем наименьшее значение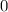 достигается при
достигается при 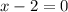 , то есть при
, то есть при 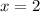
При вычитании от обеих частей неравенства одного и того же числа знак неравенства не изменяется:
Так как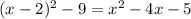 , то наименьшее значение выражения
, то наименьшее значение выражения 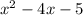 равно
равно 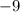 и достигается при
и достигается при