1. Алгебра
  2. Извлечь квадратный корень

Извлечь квадратный корень √(1 + ctg^2 6).

Няшка1love Няшка1love    1   18.11.2020 16:20    1

Ответы
Регина557 Регина557  18.12.2020 16:23

\sqrt{1 + \mathrm{ctg}^2 6}

Воспользовавшись формулой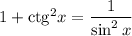 1 + \mathrm{ctg}^2 x=\dfrac{1}{\sin^2x}, получим:

\sqrt{1 + \mathrm{ctg}^2 6}=\sqrt{\dfrac{1}{\sin^26} }

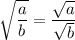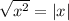Воспользовавшись формулами \sqrt{\dfrac{a}{b} } =\dfrac{\sqrt{a} }{\sqrt{b} } и \sqrt{x^2} =|x|, получим:

\sqrt{\dfrac{1}{\sin^26} }=\dfrac{1}{\sqrt{\sin^26} } =\dfrac{1}{|\sin6| }

Оценим выражение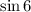 \sin6. Для этого оценим аргумент следующим образом:

4.71\approx\dfrac{3\pi}{2}

Понятно, что угол в 6 радиан располагается в 4 четверти, где синус принимает отрицательные значения. Зная это, раскроем модуль:

\dfrac{1}{|\sin6| }=\dfrac{1}{-\sin6 }=-\dfrac{1}{\sin6 }

Таким образом:

\sqrt{1 + \mathrm{ctg}^2 6}=-\dfrac{1}{\sin6 }

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
vladikn2016 vladikn2016  06.06.2019 11:10
Варифметической прогрессии . какой номер имеет член, равный 103?...
артем200412прков артем200412прков  06.06.2019 11:10
Выделите полный квадрат ,напишите,как выделяли.типо этого: больше 0 x 1. больше 0...
daurmukhtar99 daurmukhtar99  06.06.2019 11:10
Решите неравенство и укажите наибольшее целое число, удовлетворяющее этому неравенству(3-√10)x 19-6√10...
linaserdyuk13 linaserdyuk13  06.06.2019 11:10
При каких значениях переменной имеет смысл выражение: √3x-7...
Narine10 Narine10  06.06.2019 11:10
Дорога между пунктами а и в состоит из подъема и спуска, а ее длина равна 19 км. пешеход путь из а в в за 5 часов. время его движения на спуске составило 4 часа. с какой...
98675423 98675423  27.10.2020 19:57
Найдите значение выражения при a=5 b=5 6a. 34a²-b² - 2a+b​...
AbsoJl AbsoJl  27.10.2020 19:57
Можно решить все балов поставлю много...
AbrikosiK11 AbrikosiK11  27.10.2020 19:57
В чемпионате страны по футболу участвуют 16 команд. Любые две команды играют друг с другом два раза: по разу на поле каждого из соперников. Какое максимальное количество...
DIANA89320 DIANA89320  27.10.2020 19:57
Найдите координаты точек пересечения параболы с осями координат​...
andreevigor200 andreevigor200  27.10.2020 19:57
ХЕЛП АЛГЕБРА, ДОВОЛЬНО ЛЕГКО, ПРОСТО ЛЕНЬ...

Популярные вопросы