Известно, что p и p^2+2 - простые. докажите, что число p^3+2 также является простым

Question

Алгебра: Известно, что p и p^2+2 - простые. докажите, что число p^3+2 также является простым

oznobiseva2006 · Answer

Число р при делении на 3 может давать остатки 0,1 или 2.

Если число р при делении на 3 дает остаток 1, то оно имеет вид

p=3k+1, где k - некоторое целое число

Но тогда p^2+2=(3k+1)^2+2=9k^2+6k+1+2=9k^2+6k+3=3*(3k^2+2k+1) , а значит число p^2+2 не является простым. Значит такой случай невозможен

Если число р при делении на 3 дает остаток 2, то оно имеет вид

p=3k+2, где k - некоторое целое число

Но тогда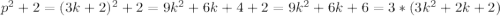 p^2+2=(3k+2)^2+2=9k^2+6k+4+2=9k^2+6k+6=3*(3k^2+2k+2) , а значит число p^2+2 не является простым. Значит такой случай невозможен

Значит число р при делении на 3 дает остаток 0, а значит число р делится нацело на 3. Число р делится нацело на 3 и является простым, значит число р может равняться только числу 3.

При р=3: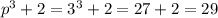 p^3+2=3^3+2=27+2=29 - простое, что и требовалось доказать.Доказано

Известно, что p и p^2+2 - простые. докажите, что число p^3+2 также является простым

Популярные вопросы