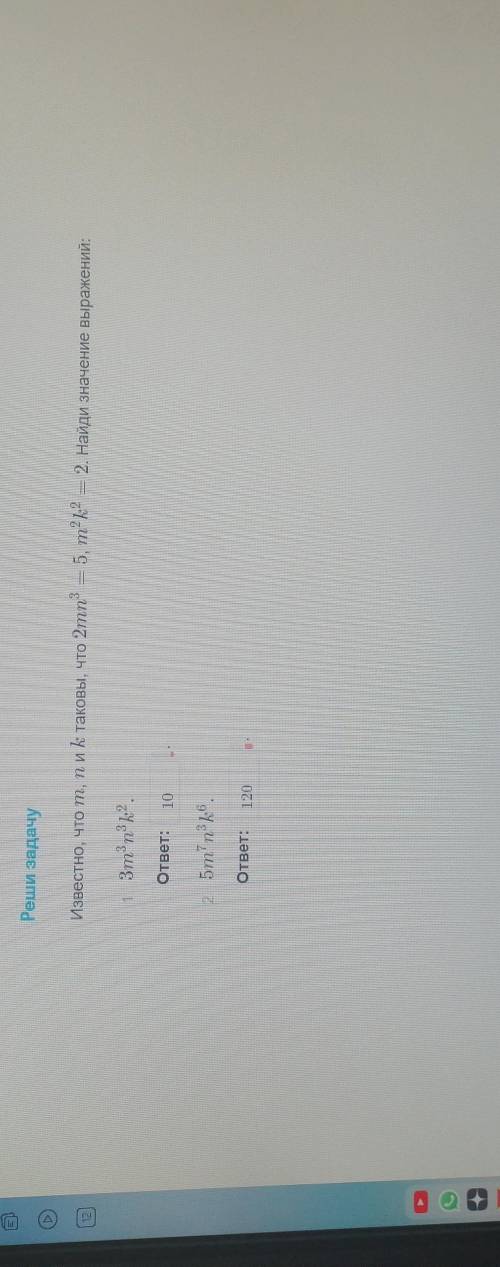
Известно, что m, n и k таковы, что 2mn^3=5, m^2 k^2=2. Найдите значение выражений: 1. 3m^3n^3k^3
ответ-10 неверно
2. 5m^7n^3k^6
ответ - 120 неверно

Я ИЗВИНЯЮСЬ ,Я НЕ ЗНАЮ ЧТО ЭТО ,ЕСЛИ БЫ МЫ ЗНАЛИ ЧТО ЭТО ТАКОЕ , МЫ БЫ ЗНАЛИ ЧТО ЭТО ТАКОЕ.

Для решения данной задачи, мы должны использовать оба уравнения, чтобы найти значения переменных m, n и k. Затем, подставив эти значения в выражения 1 и 2, мы сможем найти их значения.

В первом уравнении, 2mn^3 = 5, нам дано, что произведение чисел 2, m, n и n^3 равно 5. Мы можем разделить обе части уравнения на 2, чтобы узнать отношение между m и n^3: mn^3 = 5/2.

Во втором уравнении, m^2k^2 = 2, нам дано, что квадраты m и k равны 2. Мы можем взять квадратный корень из обеих сторон уравнения, чтобы найти значения m и k: mk = √2.

Теперь, используя полученные значения m и k, мы можем решить выражения 1 и 2:

1) 3m^3n^3k^3. Подставим значения m и k, которые у нас есть: 3(mk)^3n^3 = 3(√2)^3n^3 = 3*2√2*n^3 = 6√2n^3. Нам остается найти значение n. Используя первое уравнение: mn^3 = 5/2, можем найти n: n^3 = (5/2)/m. Тогда n = ∛[(5/2)/m]. Подставим это значение в выражение: 6√2n^3 = 6√2*∛[(5/2)/m]^3.

2) 5m^7n^3k^6. Подставим значения m и k, которые у нас есть: 5(mk)^7n^3 = 5(√2)^7n^3 = 5*2^3.5n^3 = 5*8n^3 = 40n^3. Нам остается найти значение n. Используя первое уравнение: mn^3 = 5/2, можем найти n: n^3 = (5/2)/m. Тогда n = ∛[(5/2)/m]. Подставим это значение в выражение: 40n^3 = 40*∛[(5/2)/m]^3.

Таким образом, чтобы найти значения выражений 1 и 2, нам нужно исследовать подкоренное выражение [(5/2)/m]^3 и умножить его на соответствующий коэффициент (6√2 для выражения 1 и 40 для выражения 2).

Я приведу вычисления для каждого выражения:

1) 3m^3n^3k^3 = 6√2n^3 = 6√2*∛[(5/2)/m]^3
2) 5m^7n^3k^6 = 40n^3 = 40*∛[(5/2)/m]^3.

Окончательные ответы зависят от значения [(5/2)/m]^3, которое нужно вычислить. Пожалуйста, предоставьте это значение, чтобы я мог продолжить решение.