Из пунктов а и в, расстояние между которыми равно 19 км, одновременно навстречу друг другу вышли два туриста и встретились в 10 км от пункта в. турист,шедший из а, сделал в пути получасовую остановку. найдите скорость туриста, шедшего из в, если известно, что он шел со скоростью, на 1 км/ч меньшей,чем турист, шедший из а. объясните, , как решить. , подробно распишите каждое действие.
Другие вопросы по теме Алгебра
Популярные вопросы
- Tgx*cos3x+sin3x=sin4x с подробным решением, . и число корней входящих в отрезок...
1 - Работающий по циклу карно идеальный тепловой двигатель 7/8 количества теплоты,...
3 - Дана правильная треугольная пирамида стороны основания которой равна 34 см а площадь...
1 - Найдите две дроби,каждая из которых меньше 7/15 и больше 6/17...
3 - Нам дали взять одного известного человека(в моем случае джим керри) и собрать про...
2 - Напишите значения этих слов: интернет олимпиада кросс культурный интервенция всеядный...
2 - Укажіть імя головного героя циклу міфів про аргонавтів...
2 - Найдите значение выражения: 67*10-4,5*10^2...
3 - Закон всемирного тяготения позволяет рассчитать силу взаимодействия двух тел, если...
2 - Катер,собстаенная скорость которого 12км/ч,проплыв 3 ч по течению реки и 2 ч против...
1
ответ: 5 км/ч.
Объяснение: Пусть км/ч скорость туриста шедшего из пункта В, тогда скорость туриста шедшего из пункта А будет
км/ч скорость туриста шедшего из пункта В, тогда скорость туриста шедшего из пункта А будет 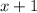 км/ч. Турист шедший из пункта В км (по условию), а турист шедший из пункта А км. Второй турист затратил времени до встречи
км/ч. Турист шедший из пункта В км (по условию), а турист шедший из пункта А км. Второй турист затратил времени до встречи 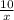 часов, а первый
часов, а первый 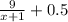 часов по условию. Т.к. оба до встречи затратили одинаковое количество времени, составим уравнение:
часов по условию. Т.к. оба до встречи затратили одинаковое количество времени, составим уравнение:
x₁=(-4) (км/ч). Не подходит, т.к. скорость не может быть отрицательной.
x₂=5 (км/ч) скорость туриста, шедшего из пункта В.