Иррациональное неравенства
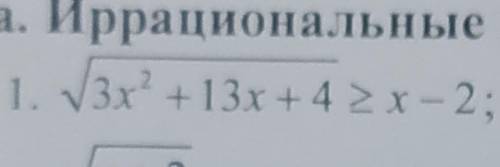
Другие вопросы по теме Алгебра
Популярные вопросы
- Кто расширяет просвет кровеносных сосудов и снижает артериальное давление?...
1 - 2808+5+(25812-1356*18)*6=по действиям...
1 - Решите уравнения: а)3y=6+2y б)6x=4x+10 а)x+2=4-x б)3x+1=5x-3 в)2x-3=2-3x...
3 - Выделите и перечислите последствие крестовых пходов на восток...
1 - Вычислите объем оксида углерода (vi) (н.у.) и массу оксида кальция,...
2 - Объясните,почему произведение 25*45 делится на 5...
3 - Переведите ! there are usually passengers and a driver in it. you don...
3 - Сколько целых чисел заключено между числами 7 и √70...
3 - Представь себя на месте своего родственника, жившего на рубиже 1920-1930-х...
3 - Представьте в виде произведения простых множителей: а) 270*252= б)...
1
1) если x-2 < 0, а подкоренное выражение неотрицательно, то неравенство верно при всех таких х, потому что арифметический квадратный корень при условии его существования всегда неторицателен и значит всегда больше отрицательного выражения справа
2)если x-2 ≥ 0
Возводим обе части неравенство в квадрат:
О т в е т. 2)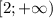
Объединяем ответы первого и второго случаев: