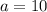Интервал (-∞:-4) является одним из решений неравенства |х2+5х+6| - 2х>a. Найди значение а и полное решение данного неравенства.
Другие вопросы по теме Алгебра
Популярные вопросы
- Са школы адначасова выйшлі Міця і Пеця. Скорасць Міці 80 м/мін, а скорасць Пеці...
3 - В теплицах вырастили одинаковое количество красных и белых роз. Красные розы развезли...
2 - Начерти ломаную, длина которой равна 1/3 части периметра квадрата с длиной стороны...
3 - На аўтамабілі з бацькамі дзеці даязджаюць да дачы за 2 г. Калі б дзеці ішлі з бацькамі...
2 - У цяпліцах вырасцілі аднолькавую колькасць чырвоных і белых руж. Чырвоныя ружы...
1 - У 9 г ад прыстані ўверх і ўніз па рацэ адышлі два катары і ў 12 г спыніліся. На...
1 - На автомобиле с родителями дети доезжают до дачи за 2 ч. Если бы дети шли с родителями...
2 - У садзе 132 грушы, а яблынь у 3 разы больш. Яблыні пасаджаны ў 6 радоў, пароўну...
1 - У школьным музеі народных рамёстваў 476 экспанатаў. Адну сёмую частку гэтых экспанатаў...
3 - Самолёт пролетел 9 мин со скоростью 15 км/мин, а следующие 9 мин — со скоростью...
3
Анализируем: решение квадратного неравенства только вида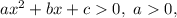 может содержать промежуток
может содержать промежуток 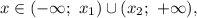 где
где 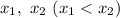 — корни квадратного уравнения
— корни квадратного уравнения 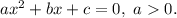
Раскроем модуль. Для этого воспользуемся правилом: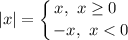
1) Пусть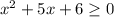
Тогда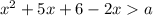
Решением исходного неравенства будет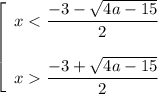
Следовательно, зная интервал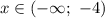 , определим значение параметра
, определим значение параметра  :
:
Таким образом,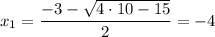 и
и 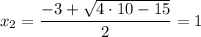
Решение: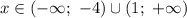
При пересечении условия модуля![x \in (-\infty; \ -3] \cup [-2; \ +\infty)](/tpl/images/1106/1316/ec0c2.png) получаем окончательное решение:
получаем окончательное решение: 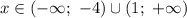 при
при 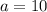
2) Если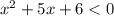 , то получаем
, то получаем 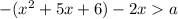 с отрицательным коэффициентом перед
с отрицательным коэффициентом перед 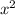 : это означает, что решением квадратного неравенства вида
: это означает, что решением квадратного неравенства вида 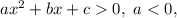 будет промежуток
будет промежуток 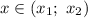 , где
, где 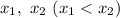 — корни квадратного уравнения
— корни квадратного уравнения 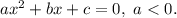 Этот случай нас не устраивает.
Этот случай нас не устраивает.
ответ: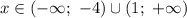 при
при