Хотябы с одним из ! 1)найдите тангенс угла наклона касательной к графику ф-ции f(x)=x^3-27 в точке пересечения этого графика с осью абсцисс. 2)найдите промежутки непрерывности ф-ции f(x)=(x^4+3x^3)/(x(x+2)) 3)материальная точка
движется по закону s(t)=12t-3t^2.найдите ее скорость и ускорение в момент времени t=1 4)напишите уравнение касательной к графику f(x)=2-x^2в точке с абциссой x=-3.выполните рисунок 5)тело выпущенное вертикально вверх со
скоростью v0 движется.

1) tga=y'(x) в некоторой точке, поэтому найдем абсциссу точки касания. Точка пересечения с осью абсцисс имеет y=0, т.е.

Найдем производную функции в точке с х=3

ответ: tga=27

2) функция прерывна в точках в которых производная не определена

найдем производную функции

Производная неопределена если ее знаменатель будет равен 0. Найдем эти значения

эти значения разбивают числовую прямую на промежутки непрерывности

(

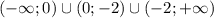
3) скорость точки это производная f'(x) уравнения движения, а ускорение - это производная от скорости движения или вторая производная f"(x)  уравнения движения в заданной точке. Надем скорость

V(1)=f'(1)=12-6t=12-6*1=6

a(1)=V'(1)=(12-6t)'=-6

4) уравнение касательной к графику функции y = f(a) + f '(a)(x – a)

f(-3)=2-(-3)^2=2-9=-7

f'(-3)=-2x=-2*(-3)=6

y=-7+6(x+3)

y=6х+11 (рисунок не могу здесь выполнить)

5) задание не полное.