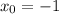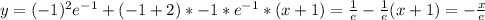Хелп,товарищи,знатоки)) задача из раздела тем (дифференциальное и интегральное исчисление)
Учитывая функцию f(x)=
А. Найдите крайние точки и экстремальные значения функции в сечении [-3;1]
Б. Найдите уравнение касательной к графику функции в точке x= -1
Другие вопросы по теме Алгебра
Популярные вопросы
- 9. Поставити у хронологічній послідовності А. Селянська війна під...
3 - В окружности с центром O отрезки AC и BD — диаметры. Вписанный...
2 - Красфорд по северной Америке 15 слов ...
1 - Put the verbs in the dialogue in the Past Simple or rhe Past Continuous.A)___(you...
3 - Сюжет повісті розгортається в такій послідовності...
3 - Маленький принц - казка про......
1 - 2 Read Liam s blog and check your ideas to Exercise 1. Then matchthe...
1 - 8 клас!! Доведіть, що ландшафт є основою структурною одиницею фізико...
2 - Определите, какое предложение не является придаточным присоединительным...
3 - Если любое задуманное число увеличить в 10 раз, от полученного вычесть...
2
Объяснение:
Крайние точки: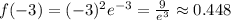 и
и 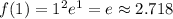
Производная функции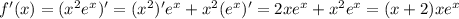
Экстремальные значения: при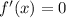 ,
, 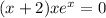 . Значит, или
. Значит, или  ,
,  , или
, или 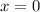 , или
, или 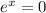 - недостижимо. Значения функции соответственно
- недостижимо. Значения функции соответственно 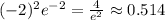 и
и 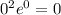
Уравнение касательной . При
. При