F(x)=tg8x-0,75x. решите неравенство если f'(x)< =0

Вопрос сформулирован некорректно. Единственное неравенство в условии  F'(x)≤0.  Другого, которое нужно решить, в условии нет.

Задача решена в следующей формулировке :

F(x)=tg8x-0,75x.  Решите неравенство   F'(x)≤0 .

Значение производной   ≥7,25, следовательно, оно не может быть отрицательным или равным нулю.

ответ : ∅

Неравенство не имеет решений

Объяснение:

Функция

F(x) = tg 8x - 0.75x

Производная  

F'(x) ≤ 0

Знаменатель производной  4cos² 8x > 0  и  cos² 8x ∈ (0; 1]

Тогда

32 - 3 cos² 8x  ≤ 0

3cos² 8x ≥ 32

cos²8x ≥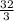 , a 32/3 > 1  чего быть не может, так как для любого угла сos²α  ∈ [0; 1].

Поэтому неравенство F'(x) ≤ 0 решений не имеет.