1. Алгебра
  2. Если для действительных положительных

Если для действительных положительных чисел а, b, c выполняются равенства ab=14 и bc=6, то найдите наименьшее значение выражения a+2b+c.​

lll38 lll38    3   19.08.2020 11:58    3

Ответы
Лера9814 Лера9814  15.10.2020 16:03

Добрый день!

4\sqrt{10}

Объяснение:

ab=14\\bc=6\\ab+bc = 20\\b(a+c) = 20\\2b(a+c) = 40

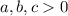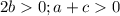
Поскольку a,b,c 0 , то 2b0 ; a+c0

Таким образом из неравенства о средних:

a+2b+c \geq 2\sqrt{2b(a+c)} = 2\sqrt{40} = 4\sqrt{10}  

Наименьшее значение достигается, когда

2b=a+c=2\sqrt{10}\\b=\sqrt{10} \\a= \frac{14}{\sqrt{10} } \\b=\frac{6}{\sqrt{10} }

Если ответ понятен, то ставь лайк и выбирай ответ лучшим!

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
IrinaArinaRina IrinaArinaRina  02.09.2019 10:40
Решите графическим систему уравнений.8 класс ....
приветик49 приветик49  02.09.2019 10:40
Одна сторона треугольника равна а, вторая сторона равна 9, а третья- в два раза меньше первой. найдите периметр треугольника. 1)p=3(x+9) 2)p=2+9 3)p=2(x+9) 4)p=3x+9...
dan4ik105217 dan4ik105217  02.09.2019 10:40
Cos2x-0,5sin2x=1 найдите самый отрицательный корень уравнения...
JoshuaJoseph JoshuaJoseph  02.09.2019 10:40
Сравните медиану и среднее арифметическое ряда чисел 5/8; 1/4; 7/16; 3/8; 7/24...
Милая8 Милая8  02.09.2019 10:40
Чему равен остаток от деления 10^1000 на 63...
annamikhaylova5 annamikhaylova5  02.09.2019 10:40
X-3/2+8-2x/5=x-10,7 решить ! ( /-это дробь)...
20042007rbn 20042007rbn  02.09.2019 10:40
Водном литре сока 80% водысксколько будет в 0.5 л....
хрустально хрустально  02.09.2019 10:40
Ну буду 4x^2-4, c-27cd^3, 16-y^2...
anonim197 anonim197  02.09.2019 10:40
Всем решить гр.пр. если b1=0,5 bn=256 q=2 надо найти n и sn...
Aidos2011 Aidos2011  02.09.2019 10:40
Подайте у вигляді добутку вираз: sin4x-sin6x...

Популярные вопросы