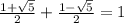Ещё одно уравнение по алгебре, только решение

Другие вопросы по теме Алгебра
Популярные вопросы
- Подскажите план, к 3 главе снежная королева...
2 - Всьавьте пропущенные слова чтобы получилось верное высказывание: : : : : для...
2 - Автомобиль ехал в город со скоростью 60 км/ч, а возвращался со скоростью 40 км/ч.какая...
3 - Необходимо разместить слова в нужном порядке, чтобы составить предложение. 1)...
1 - Восстановить словообразовательную цепочку: -безопасность надо...
2 - При каком значении а уравнение (x+2)(x--2)(x+4) = ax имеет много корней...
3 - Реферат по информатике по теме вирусы ....
1 - Назвать железы внутренней секреции и внешней секреции...
3 - Какое число нужно составить из этих цифр 3 5 6 чтобы получилось трехзначное нечётное...
2 - Як написати розповидь ти живеш помиж людей...
2
ОДЗ:
Возводим в квадрат:
Возводим в квадрат:
Замена переменной:
Обратная замена:
D=5
Оба корня входят в ОДЗ
О т в е т. cумма корней :