Докажите, что функция f возрастает на множестве R:
б)f(x) = x^5 + 4x
в) f(x) =sin x + 3x/2
Другие вопросы по теме Алгебра
Популярные вопросы
- Сөздерді мағынасына қарай cәйкестендір....
1 - чем выражены СКАЗУЕМЫЕ в данных безличных предложениях( к каждому...
2 - 924:7=, 882:6=,752 :8=,448:7=,(надо в столбик) ...
1 - Ботай тұрағынан неше тұрғын үйдің қалдықтары қазылып табылдыТАУЫП...
2 - Кроссовки, о которых мечтает Дима, стоят 6000 руб. Мама пообещала...
1 - Как делать молекулярну форму реакции...
3 - 15,8,12,10 берілген сандарды пайдаланып,пропорция құрастыр...
2 - Обчисліть і вкажіть об єм (н.у.) сульфур діоксиду, який утвориться...
2 - Сын есім заттың сынын,сапасын,түр-түсін білдіреді. Қандай?Қай? деген...
3 - БЫСТРЕЕ УМОЛЯЮ МЕНЯ МАМА УБЬЕТ СКИНУ НА КАРТУ 50 ГРИВЕН ...
1
Найдем производную:
Выражение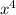 принимает только неотрицательные значения. Значит, выражение
принимает только неотрицательные значения. Значит, выражение 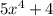 принимает только положительные значения.
принимает только положительные значения.
Таким образом, производная функции на всей области определения положительна. На промежутках, где производная положительна, функция возрастает. Значит, функция возрастает на всей области определения R.
Найдем область значений производной:
Производная принимает только положительные значения на всей области определения. На промежутках, где производная положительна, функция возрастает. Соответственно, функция возрастает на всей области определения R.