Даю 50(25)
Запишите в виде произведения
cos(π/12)+ cos(π/4)+cos(5π/6)

Ответы

Olegg9 11.10.2020 08:06

Основная формула:

$\cos\alpha+\cos\beta =2\cos\dfrac{\alpha+\beta }{2} \cos\dfrac{\alpha-\beta }{2}$

Первый вариант. Первое и второе слагаемое преобразуем в произведение, а третье преобразуем по формуле приведения. Общий множитель вынесем за скобки.

$\cos\dfrac{\pi}{12} +\cos\dfrac{\pi}{4}+\cos\dfrac{5\pi}{6}=2\cos\dfrac{\frac{\pi}{12}+\frac{\pi}{4}}{2}\cos \dfrac{\frac{\pi}{12}-\frac{\pi}{4}}{2} +\cos\dfrac{5\pi}{6}=$

$=2\cos\dfrac{\frac{\pi}{12}+\frac{3\pi}{12}}{2}\cos\dfrac{\frac{\pi}{12}-\frac{3\pi}{12}}{2} +\cos\dfrac{5\pi}{6}=2\cos\dfrac{\frac{4\pi}{12}}{2}\cos\dfrac{-\frac{2\pi}{12}}{2} +\cos\dfrac{5\pi}{6}=$

$=2\cos\dfrac{2\pi}{12}\cos\left(-\dfrac{\pi}{12}\right) +\cos\left(\pi-\dfrac{\pi}{6}\right)=2\cos\dfrac{\pi}{6}\cos\dfrac{\pi}{12}-\cos\dfrac{\pi}{6}=$

$=\boxed{\cos\dfrac{\pi}{6}\left(2\cos\dfrac{\pi}{12}-1\right)}$

Второй вариант. Добавим к выражению ноль, записанный в виде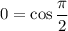 $0=\cos\dfrac{\pi}{2}$ . Преобразуем две суммы в произведения. Общий множитель опять же вынесем за скобки, но образовавшуюся в скобках сумму косинусов снова преобразуем в произведение.

В результате получим более красивое представление в виде произведения трех косинусов.

$\cos\dfrac{\pi}{12} +\cos\dfrac{\pi}{4}+\cos\dfrac{5\pi}{6}+\cos\dfrac{\pi}{2}=$

$=2\cos\dfrac{\frac{\pi}{12}+\frac{\pi}{4}}{2}\cos \dfrac{\frac{\pi}{12}-\frac{\pi}{4}}{2} +2\cos\dfrac{\frac{5\pi}{6}+\frac{\pi}{2}}{2}\cos \dfrac{\frac{5\pi}{6}-\frac{\pi}{2}}{2}=$

$=2\cos\dfrac{\frac{\pi}{12}+\frac{3\pi}{12}}{2}\cos\dfrac{\frac{\pi}{12}-\frac{3\pi}{12}}{2} +2\cos\dfrac{\frac{5\pi}{6}+\frac{3\pi}{6}}{2}\cos\dfrac{\frac{5\pi}{6}-\frac{3\pi}{6}}{2}=$

$=2\cos\dfrac{\pi}{6}\cos\dfrac{\pi}{12} +2\cos\dfrac{2\pi}{3}\cos\dfrac{\pi}{6}=2\cos\dfrac{\pi}{6}\left(\cos\dfrac{\pi}{12} +\cos\dfrac{2\pi}{3}\right)=$

$=2\cos\dfrac{\pi}{6}\cdot2\cos \dfrac{\frac{\pi}{12}+\frac{2\pi}{3}}{2} \cos \dfrac{\frac{\pi}{12}-\frac{2\pi}{3}}{2} =4\cos\dfrac{\pi}{6}\cos \dfrac{\frac{\pi}{12}+\frac{8\pi}{12}}{2} \cos \dfrac{\frac{\pi}{12}-\frac{8\pi}{12}}{2} =$