1. Алгебра
  2. Дано уравнение : используя метод

Дано уравнение : \sqrt{x+32} - 2 \sqrt[4]{x + 32 } = 3
используя метод замены переменой приведите данное уравнение к виду

2) докажите что х=49


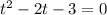
t^{2} - 2t - 3 = 0

dol2711 dol2711    3   24.12.2021 08:41    3

Ответы
kachusova2013 kachusova2013  24.12.2021 08:50

Объяснение:

\sqrt{x+32}-2*\sqrt[4]{x+32} =3\\\sqrt[4]{x+32}=t\geq 0\ \ \ \ \Rightarrow\\t^2-2t=3\\t^2-2t-3=0\\D=16\ \ \ \ \sqrt{D}=4\\t_1=\sqrt[4]{x+32} =-1\notin.\\t_2=\sqrt[4]{x+32}=3\\(\sqrt[4]{x+32} )^4=3^4\\x+32=81\\x=49.

ответ: x=49.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
kashasha kashasha  03.09.2020 05:29
( √ 324 2 ⋅ √ 0.16 0.2 ) − 6 √ 1 4 ) ÷ √ 25 ( ( 324 2 ⋅ 0.16 0.2 ) - 6 1 4 ) ÷ 25...
Настюшкаvovk Настюшкаvovk  03.09.2020 05:28
Вычислить наиболее удобным а) 1/2 + 2 2/3 + 1 1/2 + 1 1/3б) 3 2/5 * 2 3/7 * 5 * 7​...
radugraduga887 radugraduga887  03.09.2020 05:28
3 в пятой степени умножить на 6 в минус 6 степени поделить (2 в 3 степени)-4 степень....
анна2255 анна2255  03.09.2020 05:27
Определите, график какой функции изображён на рисунке. ​...
Эрбол11111 Эрбол11111  03.09.2020 05:27
Жас инженер Арман Ермеков «Жас жанұя» мемлекеттік бағдарламасы бойынша жаңа пәтер алды. Ол балалар бөлмесінің еденіне ковролан төсеуді ұйғарды. Ол үшін ұзындығы енінен екі есе...
nastya01102016 nastya01102016  03.09.2020 05:27
Докажите, что при любом значении переменной верно неравенство 1) (p — 3) (p+ 4) p(p+ 1);4) y(y + 8) (y+ 4);2) (х + 1)? х(х + 2);5) (2а – 5)2 6а? — 20a + 25;3) (а - 5)(a + 2)...
julss11 julss11  03.09.2020 05:27
Упростить уровнения 1)(5+x)*(x-2)-5x(2x+1) 2)(x+7)*(2x-3)-(x-3)*(x-6) 3)(x+2)^2+(x-4)*(x+4) 4)(y-3)*(y+4)-(y+3)^2-(8-y)*(8+y)...
КулБои КулБои  03.09.2020 05:26
Ого повторение за 7 класс​...
asimagasanova asimagasanova  03.09.2020 05:25
Нужна в решении 2ух примеров, каждый пример нужно решить по 2 разных...
ghukasyangoar ghukasyangoar  03.09.2020 05:23
Найдите все трёхзначные числа у которого вторая цифра вчетверо больше первой и на три, больше третьей, а сумма всех трёх цифр равна...

Популярные вопросы