Дано уравнение: 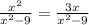$\frac{x^{2} }{x^{2} -9} =\frac{3x}{x^{2} -9}$ А) укажите область допустимых значений уравнения;
Б) приведите рациональное уравнение к квадратному уравнению;
В) найдите решения рационального уравнения

Ответы

nastasyasaenko 24.01.2021 10:21

Объяснение:

$\frac{x^2}{x^2-9}=\frac{3x}{x^2-9} .$

A) ОДЗ:

$x^2-9\neq 0\\x^2-3^2\neq 0\\(x+3)*(x-3)\neq 0\\x+3\neq 0\ \ \ \ x\neq -3;\\x-3\neq 0\ \ \ \ x\neq 3.\ \ \ \ \Rightarrow$

x∈(-∞;-3)U(-3;3)U(3;+∞).

Б)

$\frac{x^2}{x^2-9} =\frac{3x}{x^2-9}\\x^2=3x\\x^2-3x=0\\$

$x*(x-3)=0\\x_1=0 \\x-3 =0\\x_2=3\notin.$

ответ: x=0.

ПОКАЗАТЬ ОТВЕТЫ

matveibr 24.01.2021 10:21

1) Знаменатель дроби не должен равняться нулю, так как на ноль делить нельзя :

$x^{2}-9\neq 0\\\\(x-3)(x+3)\neq 0\\\\x\neq 3; \ x\neq-3\\\\\boxed{x\in(-\infty;-3)\cup(-3;3)\cup(3;+\infty)}\\\\2)\frac{x^{2} }{x^{2}-9 }=\frac{3x}{x^{2}-9}\\\\\frac{x^{2} }{x^{2}-9 }-\frac{3x}{x^{2}-9}=0\\\\\frac{x^{2}-3x }{x^{2}-9 } =0\\\\3)\left \{ {{x^{2}-3x=0 } \atop {x\neq3; \ x\neq-3}} \right.\\\\\left \{ {{x(x-3)=0} \atop {x\neq3; \ x\neq-3}} \right. \\\\\\\left \{ {{\left[\begin{array}{ccc}x_{1}=0 \\x_{2}=3-neyd \end{array}\right } \atop {x\neq 3; \ x\neq-3 }} \right.$