Числитель дроби на 3 меньше её знаменателя. сумма дроби и обратной ей дроби в 7,25 раза больше исходной дроби. найти исходную дробь. полное решение

Ответы

Владrar 11.10.2020 04:15

Исходная дробь равна $\displaystyle\frac{2}{5}$

Объяснение:

Пусть х - знаменатель дроби, тогда

(х - 3) - числитель дроби

х - целое число

$\frac{x-3}{x}$ - искомая дробь

$\frac{x}{x-3}$ - обратная дробь.

7,25 = 29/4

По условию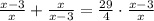 $\frac{x-3}{x} + \frac{x}{x-3} = \frac{29}{4}\cdot \frac{x-3}{x}$

$\frac{(x-3)^{2}+x^{2}}{x(x-3)}= \frac{29}{4} \cdot \frac{x-3}{x}$

$\frac{2x^{2}-6x+9 }{x-3}= \frac{29(x-3)}{4}$

8x² - 24x + 36 = 29x² - 174x + 261

21x² - 150x + 225 = 0

7x² - 50x + 75 = 0

D = 50² - 4 · 7 · 75 = 400

√D = 20

x₁ = (50 - 20)/14 = 30/14 = 15/7 - это число не является целым, поэтому не может быть знаменателем дроби

х₂ = (50 + 20)/14 = 5 - знаменатель дроби

5 - 3 = 2 - числитель дроби

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

anna18341 23.09.2019 17:50

АКА47111 23.09.2019 17:50

влад22771 23.09.2019 17:50

оля1874 23.09.2019 17:50

Yarik346 23.09.2019 17:50

Никита8547 23.09.2019 17:50

сойдет2 16.08.2019 23:50

Методом подстановки 3х+у=1 , х+2у=7...

D102006 16.08.2019 23:50

ellavinokurova 29.02.2020 19:54

Pisos1337228 29.02.2020 18:05