Биквадратные уравнения
1) х4 – 10х2 + 1=0
2) х4 + 4х решить!
Другие вопросы по теме Алгебра
Популярные вопросы
- Вы перачакаеце дождж ў хаце ці пойдзеце далей...
1 - Обведи фамилии известных людей живших в 19 веке пушкин дмитрий донской...
3 - Відредагувати словосполучення: оцінити по достоїнству, підписка на...
2 - Дан конус , высота so которого равна 10см. а радиус основания oa -3...
2 - На підставі яких природних явищ виникло првслів я: вода камінь точе,,...
1 - Как вставить в документ графическое изображение,которое хранится в...
3 - на дворе будет являться наречием или дополнением?...
3 - Какое число следует в натуральном ряду за 1999...
3 - Напишите краткое сообщение о люксембурге...
1 - Близкородственные, но не скрещивающиеся между собой виды птиц будут...
2
1)
x1 =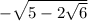
x2 =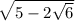
x3 =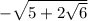
x4 =
2)
x1,2 = ±
Объяснение:
1) х² = у
у² -10у +1 = 0
D = 100 - 4 = 96
y1 = (10 -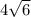 )/2 = 5 -
)/2 = 5 -  > 0
> 0
y2 = (10 +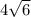 )/2 = 5 +
)/2 = 5 +  > 0
> 0
y1 = 5 -
x1 =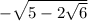
x2 =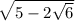
y2 = 5 +
x3 =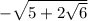
x4 =
2) х² = у
у² + 4у - 21 = 0
D = 16 + 84 = 100 = 10²
y1 = (-4-10)/2 = -7 < 0 - не интересно
y2 = (-4+10)/2 = 3 > 0
x1,2 = ±