А1. какое число не является членом арифметической прогрессии 2; 5; 8; 1) 26 2) 30 3) 44 4) 122 а2. какая из следующих последовательностей является арифметической прогрессией? 1) последовательность чисел, обратных натуральным 2) последовательность натуральных степеней чисел 3 3) последователь натуральных чисел, кратких 8 4) последовательность кубов натуральных чисел а3. последовательность задана формулой an=1-n(в квадрате). какое из указанных чисел является членом этой последовательности 1)-2 2)-3 3)-4 4)3 а4. из арифметических прогрессий выберите ту, среди членов которой есть число 8 1) an=2n+6 2) an=3n 3) an= -3n-5 4) an=3n-5 b1. первый член арифметической прогрессии равен 6, а её разность равна 4. с какого номера член этой прогрессии больше 260? с1. в арифметической прогрессии а6=-147, а7=-144. найдите номер первого положительного члена этой прогрессии.
Другие вопросы по теме Алгебра
Популярные вопросы
- У МЕНЯ СОР Напишите характеристику мужика из сказки М.Е. Салтыкова-Щедрина «...
1 - Rm of 3 Complete the sentences with for or since.1 We ve lived herethree years.2...
3 - SUMMATIVE ASSESSMENT FOR THE UNIT “ENTERTAINMENT AND MEDIA”7сlass...
2 - с текстом нужно ответить на вопросы к тексту. Choosing a profession is very difficult....
3 - Сор по геометрий 7 класс 3 четверть...
3 - Запуталась, не могу определиться. Почти не знающий или почти незнающий...
2 - 7 класс Геометрия ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️❤️...
3 - Reading. Task 1. Complete the sentences with the following words.THE LORD OF...
3 - Запиши дроби в виде процентов используя знак%24/100=12/100=34/100= ...
2 - Поставьте предложения в Past Simple или Present Perfect: 1. They (go) to the...
2
А1. Разность арифметической прогрессии: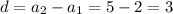
Используем формулу n-го члена арифметической прогрессии:
Число 26 является членом арифметической прогрессии.
Число 30 не является членом арифметической прогрессии, т.к. n ∉ Z
Число 44 является членом этой прогрессии
Число 122 является членом арифметической прогрессии.
ответ: 2) 30.
A2. 1) последовательность чисел, обратных натуральным: -2;-1;1;2
Здесь последовательность не является арифметической прогрессией, так как третий член должен быть 0, а не 1.
2) Нет, это геометрическая прогрессия.
3) 8; 16; 24; ... - арифметическая прогрессия, разность которой d=8
4) 1; 8; 27 - вообще не арифметическая прогрессия.
ответ: 3)
A3. Здесь нужно варианты ответов подставить вместо an.
1) -2 = 1 - n² ⇒ n² = 3 ⇔ n = ±√3 - не является
2) -3 = 1 - n² ⇒ n² = 4 ⇔ n = ±2. Здесь является только при n=2.
3) -4 = 1 - n² ⇒ n² = 5 ⇔ n = ±√5 - не является
4) 3 = 1 - n² ⇒ n² = -2 ⇔ ∅
ответ: 2) -3.
A4. Здесь подходит только an = 2n+6 так как при n=1 имеем a1=8
ответ: 1) an = 2n+6.
B1. Используем формулу n-го члена арифметической прогрессии
С номера n=65 член этой прогрессии больше 260.
C1.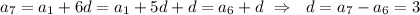
Используем снова формулу n-го члена арифметической прогрессии
n = 56 - номер первого положительного члена этой прогрессии.