А) х²+у²=25 х+у=7 б) х²у²-ху=12 х+у=2

а) второе уравнение в квадрат, вычитаем из него первое, будет 2xy=49-25=24

Имеем:

Заметим, что по теореме Виета x и y - решения уравнения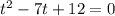

Отсюда сразу получаем ответ .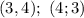

б) В первом уравнении делаем замену xy=t. Получив уравнение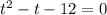 , получаем 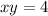или .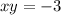

Решаем две системы:

Поступаем так же, как и в пункте а:

- для первого уравнения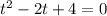 - тут корней нет.

- для второго уравнения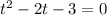

Из этого случая получаем ответ: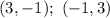

а)

1)х²+у²=25      -это окружность с центром в начале координат и r=5

2)х+у=7  y=7-x

Решение смотри на картинке(внизу)

б)заменим xy на t:
t^2 - t - 12 = 0
(t - 4)(t + 3) = 0
1) {t-4=0 { xy = 4 {2y-y^2-4=0
{x+y=0 { x=2-y {x=2-y
2y-y^2-4=0 -корней нет
2) { xy = -3 {x=2-y
{ x + y = 2 {2y-y^2=-3
x^2 - 2x - 3 = 0
(x - 3)(x + 1) = 0
x1 = 3, x2 = -1
Получаем 2 решения: (3;-1) и
(-1;3)