. 50б решить. Уравнение высших степеней.
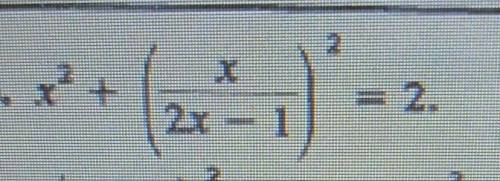
Другие вопросы по теме Алгебра
Популярные вопросы
- 2.составьте рассказ о своей частной собственности ,используя план. Смотрите картинку...
1 - Кто захочет со мной дружить? если что вот мой номер 87472512235 я девочка 13...
1 - Көп нүктенің орнына қажетті сөздер мен сөз тіркестерін қойып жаз. Помагите...
1 - 1) C:7= 2)(С:7)×9=3)К:(С:7)= решить примеры от задачи п̆̈о̆̈ӂ̈л̆̈ў̈й̆̈с̆̈т̆̈ӑ̈...
1 - Text 1. Welding & Machine Trades Welding is a skill used by many trades:...
2 - Мәтіндегі негізгі және қосымша ақпараттарды анықтай отыра, постер жасаңыз (7-8...
1 - ДАМ ЛУЧШИЙ ОТВЕТЬ ПОСТАВЛЮ ЛАЙК И ПЯТЬ ЗВЁЗД И ПОДПИШУСЬ Мәтіндерден салт етістіктерді...
3 - 1 – тапсырма. Әңгіменің кейіпкерлеріне мінездеме жазыңыз. 2 – тапсырма. Оқушылар...
1 - Не понимаю, что делать.. Выясните наибольшее значение выражения 3(5y^2−4)+(4y+3)(3−4y)...
2 - Это отрывок только. 1. Какова главная мысль рассказа Весенний дождь (Пивоваров.И)?2.Кто...
1
Объяснение: