50 . с решением на
 \geqslant 0)
Другие вопросы по теме Алгебра
Популярные вопросы
- Атаңдығы 40 кн/м серіппені 0,5 см -ге созу үшін қажетті атқарылатынжұмыс...
1 - Первое число на 50% больше второго. на сколько процентов второе число...
1 - 32. установiть вiдповiднiсть мiж словами та х творення : 1. складання...
1 - Решить двумя на стоянке п машин сначала уехало а машин а потом б сколько...
1 - Назовите несколько причин необходимости разнообразия расцветки...
1 - Напишите уравнения реакций (со структурными формулами) с сас2 с2н2...
3 - Сравните дроби: 1) 4/7 и 5/6; 2) 3/5 и 3/4; 3) 7/12 и 7/11; 4) 5/10...
2 - Пароплав проплив 24 км за течією річки і проти течії за 2 год 30 хв...
1 - Какова роль рельсов в движении поездов...
2 - Вдлинной узкой трубке с воздухом расположенной горизонтально капелька...
3
Метод рационализации: заменяем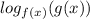 на произведение
на произведение 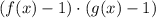 , учитывая ОДЗ .
, учитывая ОДЗ .
Смотри.............................