39
найти область определения функции
1)
$y = \frac{1}{ x\ - 12}$
2)
$y = \sqrt[12]{5 - x}$
3)
$y = \frac{1}{ \sqrt[4]{x {}^{2} } - 11x + 10}$

Ответы

alinademushkina1 10.10.2020 13:38

Решение приложено...

39 найти область определения функции1) <img src=

2) [tex]y = \sqrt[12]{5 - x" />

ПОКАЗАТЬ ОТВЕТЫ

Shoka63 10.10.2020 13:38

$\displaystyle 1. \ y=\frac{1}{x-12}$

Ограничение только на неравенство нулю знаменателя:

$x-12 \neq 0 \Rightarrow x \neq 12 \Rightarrow \boxed{x \in(-\infty; 12)\cup (12;+\infty)}$

$\displaystyle 2. \ y=\sqrt[12]{5-x}$

У нас корень четной степени, а значит, ограничением является неотрицательность подкоренного выражения:

$5-x \geq 0 \Rightarrow x \leq 5 \Rightarrow \boxed{x\in(-\infty; 5]}$

По поводу 3-его у меня сомнения в правильности записи условия:

если условие такое, как записано, то есть

$y= \dfrac{1}{\sqrt[4]{x^2}-11x+10}$ , то ограничение лишь на неравенство нулю знаменателя:

$\sqrt[4]{x^2}-11x+10 \neq 0; \sqrt[n]{x^2}=\sqrt[\frac{n}{2}]{|x|}$

В данном случае получаем:

$\sqrt{|x|}-11x+10\neq 0;$

Рассматриваем 2 случая:

$\displaystyle 1) x\geq 0: \ \sqrt{x}=t; t\geq 0; x=t^2; x\geq 0 \Rightarrow x=t^2 \Rightarrow t-11t^2+10\neq 0; \\ 11t^2-t-10\neq 0; \ (11-1-10=0) \Rightarrow \left [ {{t \neq 1} \atop {t \neq -\frac{10}{11}$

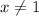
То есть $x \neq 1$

Но я сильно сомневаюсь, что там не все под корнем, рассмотрим этот случай:

$\displaystyle y=\frac{1}{\sqrt[4]{x^2-11x+10} } \Rightarrow \left \{ {{x^2-11x+10 \geq 0} \atop {x^2-11x+10\neq 0}} \right. \Rightarrow x^2-11x+100; \\ x^2-10x-x+100; x(x-10)-(x-10)0; (x-10)(x-1)0$

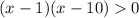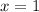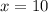Чтобы решить неравенство (x-1)(x-10)0 воспользуемся методом интервалов, нули уже нашли x=1 и x=10 , имеем +-+ на промежутках и $\boxed{x\in(-\infty;1)\cup(10;+\infty)}$