1. Алгебра
  2. 3.1. решите уравнение (х^2–3)^2–

3.1. решите уравнение (х^2–3)^2– 4(х^2–3)+3=0

annvggf annvggf    2   05.10.2019 13:01    1

Ответы
mirochkanervnya mirochkanervnya  09.10.2020 21:42
X^2-3=t
t^2-4t+3=0
D=16-4×3=16-12=4
t(1)=(4+2)/2=3
t(2)=(4-2)/2=1

x^2-3=3 x^2-3=1
x^2=6 x^2=4
x=+-√6 x=+-√4
x(1)=√6 x(2)=-√6 x(3)=2 x(4)=-2
ПОКАЗАТЬ ОТВЕТЫ
111Ботаник111 111Ботаник111  09.10.2020 21:42

Пусть (x²–3) = t, тогда (х²–3)² = t²

Получаем следующее уравнение:

t² - 4t + 3 = 0

D = b² - 4ac = 4² - 4×1×3 = 16 - 12 = 4

t1 =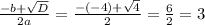 \frac{-b + \sqrt{D} }{2a} = \frac{-(-4) + \sqrt{4} }{2} =\frac{6}{2} = 3

t2 =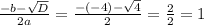 \frac{-b - \sqrt{D} }{2a} = \frac{-(-4) - \sqrt{4} }{2} =\frac{2}{2} = 1

Подставляем получившиеся корни:

1) x²–3 = 3

x² = 6

х = ±√6

2) x²–3 = 1

x² = 4

х = ±2

ответ: 2; - 2; √6; -√6.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Юлия7791 Юлия7791  28.10.2020 20:08
Десятичный эквивалент числа 11008?​...
Almira207 Almira207  28.10.2020 20:08
5 умножить на - 2/5 в 3 степени...
jojo31 jojo31  28.10.2020 20:08
При каких значениях x выражение имеет смысл: 1) 2x – 3; 2) х +3; 3) 2x2 -х – 1;2-3х24)2х-441​...
duekf duekf  28.10.2020 20:08
Нужно решить 1 вариант Все задания с обьяснениями...
belka0714 belka0714  28.10.2020 20:07
Определите коэффициент и степень одночлена​...
adwa113eПомошник adwa113eПомошник  23.09.2019 01:20
Решить с линейного уравнения с двумя переменными . : один карандаш чтоиь 60 копеек, а один блокнот - 1 руб.30 копеек. ученик купил несколько карандашей и блокнотов, заплатив за всю...
20071210 20071210  23.09.2019 01:20
3) решите неравенство 1)а) 17+х 37 1+6х 7 6х+1 0 4+х 1-2х 2+6х 5+7х...
veronekareshet veronekareshet  23.09.2019 01:20
Назови коэффициенты a, b и c линейного уравнения с двумя переменными: 4x+y−5=0 ответ: a= b= c=...
санёкмаслов санёкмаслов  23.09.2019 01:20
Внепрозрачном пакете лежат 7 красных и 5 зелёных яблок. какова вероятность того, что среди вынутых наугад из пакета трёх яблок 1 окажется зелёным, а 2 — красными?...
севга севга  23.09.2019 01:20
Решить неравенство: 25 в степени 1-3х больше или равно 1/125 найти область определения функций: у=lg 3x+1/1-3x уравнение: 4 в степени х +2*2 степени х - 80 = 0...

Популярные вопросы